��Ŀ����
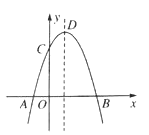
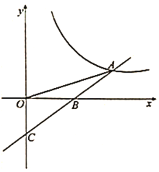
����Ŀ����ͼ����֪������![]() ����A����3��0����B��1��0����C��0��3�����㣬�䶥��ΪD���Գ�����ֱ��l��l��x�ύ�ڵ�H��
����A����3��0����B��1��0����C��0��3�����㣬�䶥��ΪD���Գ�����ֱ��l��l��x�ύ�ڵ�H��
��1����������ߵĽ���ʽ��
��2������P�Ǹ������߶Գ���l�ϵ�һ�����㣬����PBC�ܳ�����Сֵ��
��3����ͼ��2������E���߶�AD�ϵ�һ�����㣨 E��A��D���غϣ�����E����ƽ����y���ֱ�߽��������ڵ�F����x���ڵ�G�����E�ĺ�����Ϊm����ADF�����ΪS��
����S��m�ĺ�����ϵʽ��
��S�Ƿ�������ֵ�������ڣ�������ֵ����ʱ��E�����ꣻ �������ڣ���˵�����ɣ�
���𰸡��⣺��1����������![]() ����A����3��0����B��1��0����
����A����3��0����B��1��0����
�����������߽���ʽΪ![]() ��
��
����������![]() ����C��0��3������
����C��0��3������![]() ��
��
�������ߵĽ���ʽΪ��![]() ����
����![]() ��
��
��2���ߡ�PBC���ܳ�Ϊ��PB+PC+BC����BC�Ƕ�ֵ��
����PB+PC��Сʱ����PBC���ܳ���С��
����A����B���ڶԳ���I�Գƣ�
������AC��l�ڵ�P������PΪ����ĵ㡣
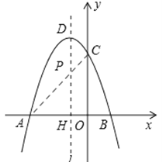
��AP=BP�����PBC���ܳ���С�ǣ�PB+PC+BC=AC+BC��
��A����3��0����B��1��0����C��0��3������AC=3![]() ��BC=
��BC=![]() ��
��
���PBC���ܳ���С�ǣ�![]() ��
��
��3���١�������![]() ����D������Ϊ����1��4����A����3��0����
����D����������1��4����A����3��0����
��ֱ��AD�Ľ���ʽΪy=2x+6
����E�ĺ�����Ϊm����E��m��2m+6����F��m��![]() ��
��
��![]() ��
��
��![]() ��
��
��S��m�ĺ�����ϵʽΪ![]() ��
��
��![]() ��
��
����m=��2ʱ��S������ֵΪ1����ʱ��E������Ϊ����2��2����
����������1�����ݺ���ͼ�������㣬�ô���ϵ����ȷ�����κ����Ľ���ʽ���ɡ�
��2������BC�Ƕ�ֵ���õ���PB+PC��Сʱ����PBC���ܳ���С�����ݵ�����������Ӧ�߶εij����ɡ�
��3�����E�ĺ�����Ϊm����ʾ��E��m��2m+6����F��m��![]() ��������ʾ��EF�ij����Ӷ���ʾ��S��m�ĺ�����ϵ��Ȼ������κ�������ֵ���ɡ�
��������ʾ��EF�ij����Ӷ���ʾ��S��m�ĺ�����ϵ��Ȼ������κ�������ֵ���ɡ�

 һ����ʦ�����Ծ�ϵ�д�
һ����ʦ�����Ծ�ϵ�д� �����Ծ���Ԫ���Ծ�ϵ�д�
�����Ծ���Ԫ���Ծ�ϵ�д�