题目内容
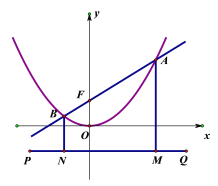
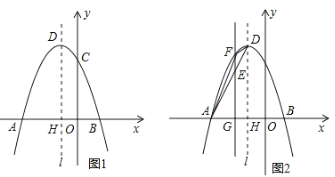
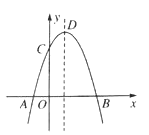
【题目】如图,抛物线y=-x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个判断:①当x>0时,y>0;②若a=-1,则b=3;③抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1<x2,且x1+x2>2,则y1>y2;④点C关于抛物线对称轴的对称点为E,点G、F分别在x轴和y轴上,当m=2时,四边形EDGF周长的最小值为![]() ,其中,判断正确的序号是( )
,其中,判断正确的序号是( )
A.①②B.②③C.①③D.②③④
【答案】B
【解析】
根据抛物线在x轴上方所对应的自变量的范围可判断①;先求出抛物线的对称轴,利用抛物线的对称性求出b可判断②;先求出抛物线的对称轴,然后比较点P和Q到对称轴距离的大小,然后可以确定函数值的大小,即可判断③;先求出D、E两点的坐标,然后求出符合题意的对称点坐标分别为(-1,4)(2,-3),然后根据勾股定理计算即可判断④.
①当x>0时,y不一定大于0,故错误;
②对称轴为1,当a=-1,b=3,故正确;
③![]() >1,∴
>1,∴![]()
Q点距离对称轴较远,∴y1>y2,故正确;
④m=2时,D(1,4),E(2,3),
可得出DE的对称点为(-1,4)(2,-3),
四边形DEFG的周长为![]() ,故错误;
,故错误;
故答案为:B.

练习册系列答案
相关题目