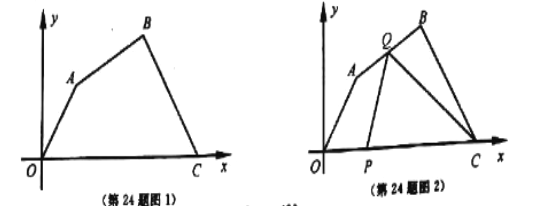题目内容
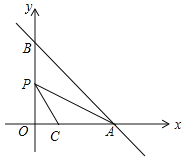
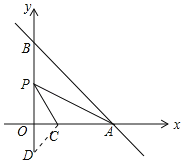
【题目】如图,在平面直角坐标系xOy中,直线y=﹣x+m分别交x轴,y轴于A,B两点,已知点C(2,0).
(1)当直线AB经过点C时,点O到直线AB的距离是 ;
(2)设点P为线段OB的中点,连结PA,PC,若∠CPA=∠ABO,则m的值是 .
【答案】(1)![]() ;(2)12.
;(2)12.
【解析】
试题分析:(1)当直线AB经过点C时,点A与点C重合,当x=2时,y=﹣2+m=0,即m=2,所以直线AB的解析式为y=﹣x+2,则B(0,2),∴OB=OA=2,AB=![]() .
.
设点O到直线AB的距离为d,由S△OAB=![]() OA2=
OA2=![]() ABd,得:4=
ABd,得:4=![]() d,则d=
d,则d=![]() .故答案为:
.故答案为:![]() .
.
(2)作OD=OC=2,连接CD.则∠PDC=45°,如图,由y=﹣x+m可得A(m,0),B(0,m).
所以OA=OB,则∠OBA=∠OAB=45°.
当m<0时,∠APC>∠OBA=45°,所以,此时∠CPA>45°,故不合题意.
所以m>0.
因为∠CPA=∠ABO=45°,所以∠BPA+∠OPC=∠BAP+∠BPA=135°,即∠OPC=∠BAP,则△PCD∽△APB,所以![]() ,即
,即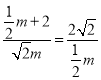 ,解得m=12.故答案为:12.
,解得m=12.故答案为:12.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目