Question

【题目】如图，将边长为6的正方形沿其对角线剪开，再把沿着方向平移，得到，当两个三角形重叠部分的面积为5时，则为______.

Answer 1

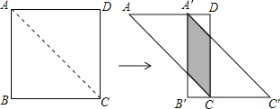
【答案】1或5

【解析】

设AA′=x，AC与A′B′相交于点E，判断出△AA′E是等腰直角三角形，根据等腰直角三角形的性质可得A′E=x，再表示出A′D，然后根据平行四边形的面积公式列方程求解即可．

设AA′=x，AC与A′B′相交于点E，
∵△ACD是正方形ABCD剪开得到的，
∴△ACD是等腰直角三角形，
∴∠A=45°，
∴△AA′E是等腰直角三角形，
∴A′E=AA′=x，
A′D=AD-AA′=6-x，
∵两个三角形重叠部分的面积为5，
∴x（6-x）=5，
整理得，x2-6x+5=0，
解得x1=1，x2=5，
即移动的距离AA′等于1或5．
故答案是：1或5．