题目内容
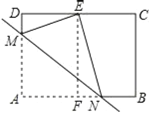
【题目】如图,二次函数![]() 与x轴交于点B和点A(-1,0),与y轴交于点C,与一次函数
与x轴交于点B和点A(-1,0),与y轴交于点C,与一次函数![]() 交于点A和点D.
交于点A和点D.

1.求出![]() 的值;
的值;
2.若直线AD上方的抛物线存在点E,可使得△EAD面积最大,求点E的坐标;
3.点F为线段AD上的一个动点,点F到(2)中的点E的距离与到y轴的距离之和记为d,求d的最小值及此时点F的坐标.
【答案】(1)a=1;b=3;c=4. (2)当m=1时,最大值为6,此时点E的坐标为(1,6)(3)d的最小值为5,F点的坐标为(1,2).
【解析】
(1)根据图形可以看出点C的坐标为(0,4),点B的坐标为(4,0),代入二次函数的解析式中,即可得出b、c的值,将点A(-1,0)代入一次函数中,即可求得a的值;
(2)设点E的横坐标为m,则可得出点E的纵坐标为-m2+3m+4.过点E作x轴的垂线l,交x轴于点G,交AD于点H,则点H的坐标为(m,m+1).过点D作l的垂线,垂足为T;联立直线方程和二次函数方程,即可得出D的坐标,再根据S△AED=S△AEH+S△HED,得出含m的函数,利用a的取值范围,可知,当m=1时,即可得出最大值,从而可得出E的坐标;
(3)过A作y轴的平行线AS,过F作FG⊥y轴交AS于点M,过F作FN⊥x轴于N,结合已知,可得出FM=FN,即有d=FE+FM-1=FE+FN-1,可知当N、F、E所在直线与x轴垂直时,d=FE+FN-1最小,即可得出F的坐标.
(1)∵点C(0,4),B(4,0)在函数的图象上,
∴![]()
解得:b=3,c=4,
∵点A(-1,0)在一次一次函数y=x+a上,
∴0=-1+a,
∴a=1.
所以a=1,b=3,c=4.
(2)设点E的横坐标为m,则点E的纵坐标为![]() .过点E作x轴的垂线l,交x轴于点G,交AD于点H,则点H的坐标为
.过点E作x轴的垂线l,交x轴于点G,交AD于点H,则点H的坐标为![]() .过点D作l的垂线,垂足为T.
.过点D作l的垂线,垂足为T.
将![]() 与
与![]() 联立组成方程组,解得点D的坐标为(3,4).
联立组成方程组,解得点D的坐标为(3,4).
所以![]()
![]()
![]()
![]()
∵a=![]() <0,
<0,
∴![]() 有最大值.当m=1时,最大值为6,此时点E的坐标为(1,6)
有最大值.当m=1时,最大值为6,此时点E的坐标为(1,6)
(3)过A作y轴的平行线AS,过F作FG⊥y轴交AS于点M,过F作FN⊥x轴于N,如图所示:
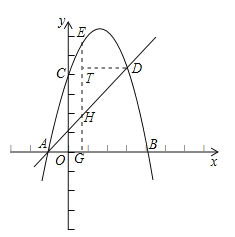
∵点D的坐标为(3,4),点A坐标为(-1,0)
∴∠DAB=45°
∴AD平分∠SAB,
∴FM="FN"
∴d =FE+FM-1=FE+FN-1
显然,当N、F、E所在直线与x轴垂直时,d=FE+FN-1最小,最小值为6-1=5.
此时点F的横坐标为1,代入![]() 得F点的坐标为(1,2).
得F点的坐标为(1,2).