题目内容
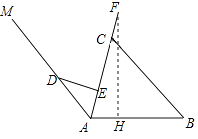
【题目】为缓解交通拥堵，减少环境污染，倡导低碳出行，构建慢行交通体系，南浔中心城区正在努力建设和完善公共自行车服务系统．图1所示的是一辆自行车的实物图．图2是自行车的车架示意图．CE=30cm，DE=24cm，AD=26cm，DE⊥AC于点E，座杆CF的长为20cm，点A、E、C、F在同一直线上，且∠CAB=75°． 
（1）求车架中AE的长；
（2）求车座点F到车架AB的距离．（结果精确到1cm，参考数据：sin75°≈0.97，cos75°≈0.26，tan75°≈3.73）
【答案】
（1）解：在Rt△ADE中，由勾股定理得，
AE= 
= 
=10（cm）
（2）解：如图所示：过点F作FH⊥AB于H，
在Rt△AFH中，
sin∠FAH= 
，
∵AF=AE+CE+CF=10+30+20=60（cm）．
∴FH=AFsin∠FAH=60sin75°≈60×0.97=58.2（cm）．
答：车座点F到车架AB的距离为58.2cm．
【解析】（1）根据勾股定理求出AE的长；（2）作FH⊥AB于H，求出AF的长，根据正弦的概念求出点E到车架AB的距离．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
