��Ŀ����
����Ŀ����ͼ��OABC��ƽ���ı��Σ��Խ���OB�����������ϣ�λ�ڵ�һ���ĵ�A�͵ڶ����ĵ�C�ֱ���˫����y= ![]() ��y=
��y= ![]() ��һ֧�ϣ��ֱ����A��C��x��Ĵ��ߣ�����ֱ�ΪM��N���������µĽ��ۣ�
��һ֧�ϣ��ֱ����A��C��x��Ĵ��ߣ�����ֱ�ΪM��N���������µĽ��ۣ�
�� ![]() =
= ![]() ��
��
����Ӱ��������� ![]() ��k1+k2����
��k1+k2����
�۵���AOC=90��ʱ��|k1|=|k2|��
����OABC�����Σ�����˫���ȹ���x��Գƣ�Ҳ����y��Գƣ�
������ȷ�Ľ���������������ȷ�Ľ��۵���Ŷ����ϣ���
���𰸡��٢�
���������⣺��AE��y����E��CF��y����F����ͼ��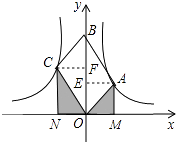
���ı���OABC��ƽ���ı��Σ�
��S��AOB=S��COB ��
��AE=CF��
��OM=ON��
��S��AOM= ![]() |k1|=
|k1|= ![]() OMAM��S��CON=
OMAM��S��CON= ![]() |k2|=
|k2|= ![]() ONCN��
ONCN��
�� ![]() =
= ![]() ���ʢ���ȷ��
���ʢ���ȷ��
��S��AOM= ![]() |k1|��S��CON=
|k1|��S��CON= ![]() |k2|��
|k2|��
��S��Ӱ����=S��AOM+S��CON= ![]() ��|k1|+|k2|����
��|k1|+|k2|����
��k1��0��k2��0��
��S��Ӱ����= ![]() ��k1��k2�����ʢڴ���
��k1��k2�����ʢڴ���
����AOC=90�㣬
���ı���OABC�Ǿ��Σ�
���ȷ��OA��OC��ȣ�
��OM=ON��
����жϡ�AOM�ա�CNO��
����ж�AM=CN��
���ȷ��|k1|=|k2|���ʢ۴���
��OABC��������OA=OC��
��OM=ON��
��Rt��AOM��Rt��CNO��
��AM=CN��
��|k1|=|k2|��
��k1=��k2 ��
����˫���ȹ���x��Գƣ�Ҳ����y��Գƣ��ʢ���ȷ��
�ʴ�Ϊ���٢ܣ�
��AE��y���ڵ�E��CF��y���ڵ�F������ƽ���ı��ε����ʵ�S��AOB=S��COB �� ���������������ʽ�õ�AE=CF������OM=ON�������÷���������k�ļ�������������������ʽ�õ�S��AOM= ![]() |k1|=
|k1|= ![]() OMAM��S��CON=
OMAM��S��CON= ![]() |k2|=
|k2|= ![]() ONCN��������
ONCN�������� ![]() =
= ![]() ����S��AOM=
����S��AOM= ![]() |k1|��S��CON=
|k1|��S��CON= ![]() |k2|���õ�S��Ӱ����=S��AOM+S��CON=
|k2|���õ�S��Ӱ����=S��AOM+S��CON= ![]() ��|k1|+|k2|��=
��|k1|+|k2|��= ![]() ��k1��k2��������AOC=90�㣬�õ��ı���OABC�Ǿ��Σ����ڲ���ȷ��OA��OC��ȣ������жϡ�AOM�ա�CNO�����Բ����ж�AM=CN������ȷ��|k1|=|k2|����OABC�����Σ��������ε����ʵ�OA=OC�����ж�Rt��AOM��Rt��CNO����AM=CN������|k1|=|k2|����k1=��k2 �� ���ݷ��������������ʵ���˫���ȹ���x��Գƣ�Ҳ����y��Գƣ�
��k1��k2��������AOC=90�㣬�õ��ı���OABC�Ǿ��Σ����ڲ���ȷ��OA��OC��ȣ������жϡ�AOM�ա�CNO�����Բ����ж�AM=CN������ȷ��|k1|=|k2|����OABC�����Σ��������ε����ʵ�OA=OC�����ж�Rt��AOM��Rt��CNO����AM=CN������|k1|=|k2|����k1=��k2 �� ���ݷ��������������ʵ���˫���ȹ���x��Գƣ�Ҳ����y��Գƣ�