题目内容
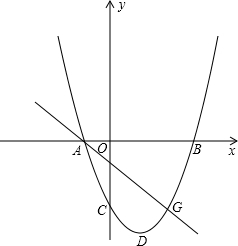
如图,抛物线y=x2+bx+c经过点(1,-4)和(-2,5),请解答下列问题:(1)求抛物线的解析式;
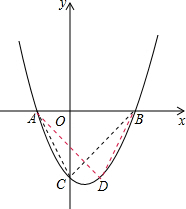
(2)若与x轴的两个交点为A、B,与y轴交于点C.在该抛物线上找一点D,使得△ABC与△ABD全等,求出D点的坐标.
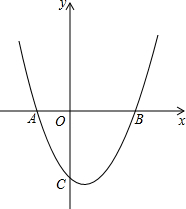
(2)若与x轴的两个交点为A、B,与y轴交于点C.在该抛物线上找一点D,使得△ABC与△ABD全等,求出D点的坐标.

(1)由题意,得
,
解得,
,
所以,该抛物线的解析式为:y=x2-2x-3;
(2)∵抛物线y=x2-2x-3的对称轴为:x=-
=1,
∴根据轴对称的性质,点C关于x=1的对称点D即为所求,
此时,AC=BD,BC=AD,
在△ABC和△BAD中,
∵
,
∴△ABC≌△BAD(SSS).
在y=x2-2x-3中,令x=0,得y=-3,
则C(0,-3),
∴D(2,-3).
|
解得,
|
所以,该抛物线的解析式为:y=x2-2x-3;
(2)∵抛物线y=x2-2x-3的对称轴为:x=-
| -2 |
| 2×1 |
∴根据轴对称的性质,点C关于x=1的对称点D即为所求,
此时,AC=BD,BC=AD,
在△ABC和△BAD中,
∵
|
∴△ABC≌△BAD(SSS).
在y=x2-2x-3中,令x=0,得y=-3,
则C(0,-3),
∴D(2,-3).


练习册系列答案
相关题目

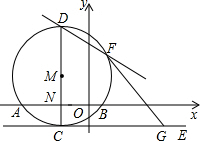 直于x轴于N,直线CE切圆M于C,直线FG切圆M于F,交CE于G,已知点G的横坐标为3,
直于x轴于N,直线CE切圆M于C,直线FG切圆M于F,交CE于G,已知点G的横坐标为3,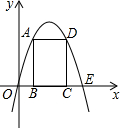
 x轴交于A、B两点,其中B点的坐标为(3,0),且OB=OC.
x轴交于A、B两点,其中B点的坐标为(3,0),且OB=OC.


