题目内容
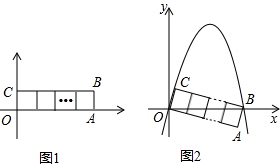
如图,矩形ABCD的顶点B、C在x轴上,A、D在抛物线y=ax2+bx上,且y=ax2+bx的最大值是2,y=ax2+bx与x轴的正半轴的交点E的坐标是(2,0).
(1)求a,b的值;
(2)若矩形的顶点均为动点,且矩形在抛物线与x轴围成的封闭区域内,试探索:是否存在周长为3的矩形?若存在,求出此时B点的坐标;若不存在说明理由.
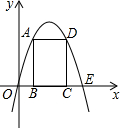
(1)求a,b的值;
(2)若矩形的顶点均为动点,且矩形在抛物线与x轴围成的封闭区域内,试探索:是否存在周长为3的矩形?若存在,求出此时B点的坐标;若不存在说明理由.
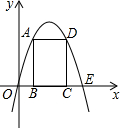
(1)根据题意得:抛物线y=ax2+bx过点(2,0),(1,2),
∴
,
解得:
;
(2)由(1)得:抛物线的解析式为:y=-2x2+4x,
设点A(m,n),则BC=2-2m,BA=-2m2+4m,
∴矩形的周长为:2(AB+BC)=2(2-2m-2m2+4m)=-4m2+4m+4,
若存在周长为3的矩形ABCD,则:
-4m2+4m+4=3,
即-4m2+4m+1=0,
解得:m=
,
∵m=
<0不符合题意,舍去,
∴m=
,
∴存在周长为3的矩形,此时B点的坐标为:(
,0).
∴
|
解得:
|
(2)由(1)得:抛物线的解析式为:y=-2x2+4x,
设点A(m,n),则BC=2-2m,BA=-2m2+4m,
∴矩形的周长为:2(AB+BC)=2(2-2m-2m2+4m)=-4m2+4m+4,
若存在周长为3的矩形ABCD,则:
-4m2+4m+4=3,
即-4m2+4m+1=0,
解得:m=
1±
| ||
| 2 |
∵m=
1-
| ||
| 2 |
∴m=
1+
| ||
| 2 |
∴存在周长为3的矩形,此时B点的坐标为:(
1+
| ||
| 2 |

练习册系列答案
相关题目
 +bx+c(a<0),如果抛物线同时经过点O、B、C:
+bx+c(a<0),如果抛物线同时经过点O、B、C: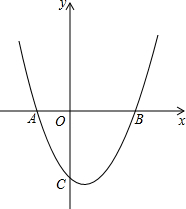

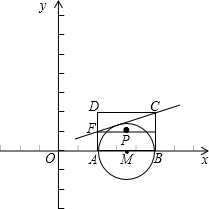 半轴上,点A在点B的左侧,另两个顶点都在第一象限,且直线
半轴上,点A在点B的左侧,另两个顶点都在第一象限,且直线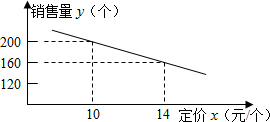 个星期的销售量y(个)与它的定价x(元/个)的关系如图所示:
个星期的销售量y(个)与它的定价x(元/个)的关系如图所示: x的图象交于O、A两点.
x的图象交于O、A两点.