题目内容
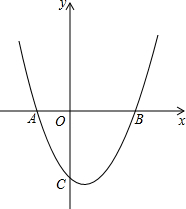
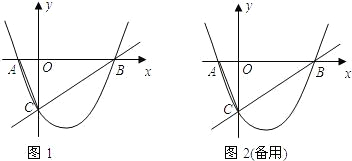
如图,二次函数y=ax2+bx+c的图象与x轴交于两个不同的点A(-2,0)、B(4,0),与y轴交于点C(0,3),连接BC、AC,该二次函数图象的对称轴与x轴相交于点D.
(1)求这个二次函数的解析式、点D的坐标及直线BC的函数解析式;
(2)点Q在线段BC上,使得以点Q、D、B为顶点的三角形与△ABC相似,求出点Q的坐标;
(3)在(2)的条件下,若存在点Q,请任选一个Q点求出△BDQ外接圆圆心的坐标.

(1)求这个二次函数的解析式、点D的坐标及直线BC的函数解析式;
(2)点Q在线段BC上,使得以点Q、D、B为顶点的三角形与△ABC相似,求出点Q的坐标;
(3)在(2)的条件下,若存在点Q,请任选一个Q点求出△BDQ外接圆圆心的坐标.

(1)∵二次函数y=ax2+bx+c的图象与x轴交于两个不同的点A(-2,0)、B(4,0),
与y轴交于点C(0,3),
∴设二次函数为y=a(x+2)(x-4),把点C(0,3)代入得,a(0+2)(0-4)=3,
解得a=-
,
∴这个一次函数的解析式为:y=-
x2+
x+3;
∵y=-
x2+
x+3=-
(x-1)2+
,
∴抛物线的对称轴是直x=1,
∴点D的坐标为(1,0).
设直线BC的解析式为;y=kx+b(k≠0),
∴
,解得
,
∴直线BC的解析式为y=-
x+3.
(2)∵A(-2,0),B(4,0),C(0,3),D(1,0),
∴OD=1,BD=3,CO=3,BO=4,AB=6,
∴BC=
=
=5,
如图1,当∠QDB=∠CAB时,
=
,
=
,解得QB=
过点Q作QH⊥x轴于点H,
∵OC⊥x轴,
∴QH∥CO.
∴
=
.解得QH=
.
把y=
代入y=-
x+3,得x=2.
∴此时,点Q的坐标为(2,
);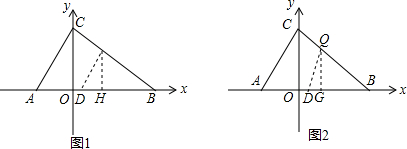
如图2,当∠DQB=∠CAB时,
=
,即
=
,得QB=
.
过点Q作QG⊥x轴于点G,
∵OC⊥x轴,
∴QG∥CO.
∴
=
.解得QG=
.
把y=
代入y=-
x+3,得x=
.
∴此时,点Q的坐标为(
,
).
综上所述,点Q坐标为(2,
)或(
,
);
(3)当点Q的坐标为(2,
)时,设圆心的M(
,y).
∵MD=MQ,
∴(
-1)2+y2=(
-2)2+(y-
)2,解得y=
,
∴M(
,
).
与y轴交于点C(0,3),
∴设二次函数为y=a(x+2)(x-4),把点C(0,3)代入得,a(0+2)(0-4)=3,
解得a=-
| 3 |
| 8 |
∴这个一次函数的解析式为:y=-
| 3 |
| 8 |
| 3 |
| 4 |
∵y=-
| 3 |
| 8 |
| 3 |
| 4 |
| 3 |
| 8 |
| 27 |
| 8 |
∴抛物线的对称轴是直x=1,
∴点D的坐标为(1,0).
设直线BC的解析式为;y=kx+b(k≠0),
∴
|
|
∴直线BC的解析式为y=-
| 3 |
| 4 |
(2)∵A(-2,0),B(4,0),C(0,3),D(1,0),
∴OD=1,BD=3,CO=3,BO=4,AB=6,
∴BC=
| OB2+OC2 |
| 42+32 |
如图1,当∠QDB=∠CAB时,
| QB |
| CB |
| DB |
| AB |
| QB |
| 5 |
| 3 |
| 6 |
| 5 |
| 2 |
过点Q作QH⊥x轴于点H,
∵OC⊥x轴,
∴QH∥CO.
∴
| QH |
| 3 |
| ||
| 5 |
| 3 |
| 2 |
把y=
| 3 |
| 2 |
| 3 |
| 4 |
∴此时,点Q的坐标为(2,
| 3 |
| 2 |
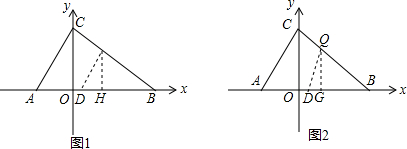
如图2,当∠DQB=∠CAB时,
| QB |
| AB |
| DB |
| CB |
| QB |
| 6 |
| 3 |
| 5 |
| 18 |
| 5 |
过点Q作QG⊥x轴于点G,
∵OC⊥x轴,
∴QG∥CO.
∴
| QG |
| 3 |
| ||
| 5 |
| 54 |
| 25 |
把y=
| 54 |
| 25 |
| 3 |
| 4 |
| 28 |
| 25 |
∴此时,点Q的坐标为(
| 28 |
| 25 |
| 54 |
| 25 |
综上所述,点Q坐标为(2,
| 3 |
| 2 |
| 28 |
| 25 |
| 54 |
| 25 |
(3)当点Q的坐标为(2,
| 3 |
| 2 |
| 5 |
| 2 |
∵MD=MQ,
∴(
| 5 |
| 2 |
| 5 |
| 2 |
| 3 |
| 2 |
| 1 |
| 12 |
∴M(
| 5 |
| 2 |
| 1 |
| 12 |

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
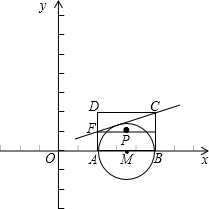 半轴上,点A在点B的左侧,另两个顶点都在第一象限,且直线
半轴上,点A在点B的左侧,另两个顶点都在第一象限,且直线
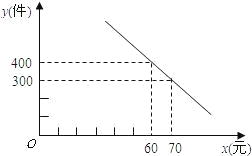 间的函数关系式,并写出自变量x的取值范围;根据题意判断:当x取何值时,P的值最大,最大值是多少?
间的函数关系式,并写出自变量x的取值范围;根据题意判断:当x取何值时,P的值最大,最大值是多少?