Question

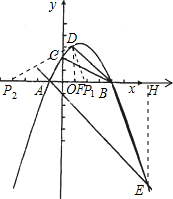
设抛物线y=ax²+bx+c与x轴交于两个不同的点A（-l，0）、B（4，0），与y轴交于点C（0，2）．
（1）求抛物线的解析式：
（2）问抛物线上是否存在一点M，使得S_△ABM=2S_△ABC？若存在，求出点M的坐标；若不存在，请说明理由．
（3）已知点D（1，n）在抛物线上，过点A的直线y=-x-1交抛物线于另一点E．
①求tan∠ABD的值：
②若点P在x轴上，以点P、B、D为顶点的三角形与△AEB相似，求点P的坐标．

Answer 1

（1）把三点分别代入后求解可得：
a=-

1

2

，b=

3

2

，c=2；
代入后得此函数解析式为：y=-

1

2

x2+

3

2

x+2；

（2）假设存在这样的点M，使得S_△ABM=2S_△ABC
假设点M的坐标为：（x_M，y_M），
所以有：

1

2

•AB•h=2•

1

2

•AB•2，
其中h是三角形ABM AB 边上的高等于y_M的绝对值，解得h=4，
二次函数解析式y=-

1

2

x2+

3

2

x+2的最大值是3

1

8

＜4，
故x轴的上方不存在这样的M点，
所以有y_M=-4，即有y=-

1

2

x2+

3

2

x+2=-4，
解得：x=

3+ 57

2

或者

3- 57

2

，
即M点的坐标为（

3+ 57

2

，-4）或者（

3- 57

2

，-4）；

（3）①D（1，n）代入原函数解析式得：n=3
所以D点坐标为（1，3），
过点D作垂线DF⊥x轴，可得tan∠ABD=

3

4-1

=1，
②由y=-x-1和y=-

1

2

x2+

3

2

x+2；联立求解得：
x=-1 y=0 或者 x=6 y=-7；
所以点E的坐标为（6，-7），
过点E作EH⊥x轴于H，则H（6，0），
所以AH=EH=7，∠EAH=45°，又因为tan∠ABD=

3

4-1

=1，故∠DBF=45°
所以∠EAH=∠DBF，且有∠DBH=135°
90°＜∠EBA＜135°，则点P只能在点B的左侧，即有以下两种情况：
1）△DBP∽△EAB，则有：

BP

AB

=

BD

AE

，
所以BP=

AB•BD

AE

=

15

7

，故OP=4-

15

7

=

13

7

，
所以点P坐标为（

13

7

，0）
2）△DBP∽△BAE，则有

BP

AE

=

BD

AB

，
所以BP=

AE•BD

AB

=

42

5

，
OP=

42

5

-4=

22

5

，
所以点P的坐标为（-

22

5

，0），
综上所述点P坐标为（

13

7

，0）或者（-

22

5

，0）．