题目内容
如图,圆M与x轴相交于A,B两点,其坐标分别为A(-3,0),B(1,0),直径CD垂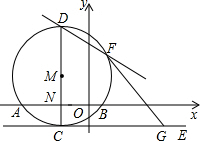 直于x轴于N,直线CE切圆M于C,直线FG切圆M于F,交CE于G,已知点G的横坐标为3,
直于x轴于N,直线CE切圆M于C,直线FG切圆M于F,交CE于G,已知点G的横坐标为3,
(1)若抛物线y=-x2-2x+m经过A,B,D三点,求m的值及点D的坐标;
(2)求直线DF的解析式;
(3)是否存在过点G的直线,使它与(1)中抛物线的两个交点的横坐标之和等于4?若存在,请求出满足条件的直线的解析式;若不存在,请说明理由.
 直于x轴于N,直线CE切圆M于C,直线FG切圆M于F,交CE于G,已知点G的横坐标为3,
直于x轴于N,直线CE切圆M于C,直线FG切圆M于F,交CE于G,已知点G的横坐标为3,(1)若抛物线y=-x2-2x+m经过A,B,D三点,求m的值及点D的坐标;
(2)求直线DF的解析式;
(3)是否存在过点G的直线,使它与(1)中抛物线的两个交点的横坐标之和等于4?若存在,请求出满足条件的直线的解析式;若不存在,请说明理由.
(1)∵抛物线y=-x2-2x+m过点A,B两点,
∴-3×1=-m,
∴抛物线为y=-x2-2x+3,
又∵抛物线过点D,由圆的对称性知点D为抛物线的顶点,
∴D点坐标为(-1,4).
(2)由题意知AB=4,
∵CD⊥x轴,
∴NA=NB=2,
∴ON=1,
由相交弦定理得NA•NB=ND•NC,
∴NC×4=2×2,NC=1,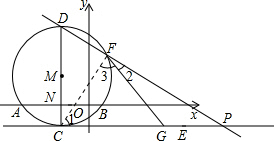
∴C的坐标为(-1,-1),
设直线DF交CE于P,连接CF,得∠CFP=90°,
∵CG,FG为圆M的切线,
∴FG=GC,
∴∠1=∠3,
∴∠2=∠FPC,
∴FG=GP,
∴GC=GP,
可得CP=8,
∴P点的坐标为(7,-1);
设直线DF的解析式为y=kx+b(k≠0),
则
解得
∴直线DF的解析式为y=-
x+
;
(3)假设存在过G的直线y=k1x+b1,
则3k1+b1=-1,
∴b1=-3k1-1,
解方程组
,
得x2+(2+k1)x-3k1-4=0,
由题意得-2-k1=4,
∴k1=-6,
∴△=-40<0,
∴方程无实数根,
∴方程组无实数解;
∴满足条件的直线不存在.
∴-3×1=-m,
∴抛物线为y=-x2-2x+3,
又∵抛物线过点D,由圆的对称性知点D为抛物线的顶点,
∴D点坐标为(-1,4).
(2)由题意知AB=4,
∵CD⊥x轴,
∴NA=NB=2,
∴ON=1,
由相交弦定理得NA•NB=ND•NC,
∴NC×4=2×2,NC=1,

∴C的坐标为(-1,-1),
设直线DF交CE于P,连接CF,得∠CFP=90°,
∵CG,FG为圆M的切线,
∴FG=GC,
∴∠1=∠3,
∴∠2=∠FPC,
∴FG=GP,
∴GC=GP,
可得CP=8,
∴P点的坐标为(7,-1);
设直线DF的解析式为y=kx+b(k≠0),
则
|
解得
|
∴直线DF的解析式为y=-
| 5 |
| 8 |
| 27 |
| 8 |
(3)假设存在过G的直线y=k1x+b1,
则3k1+b1=-1,
∴b1=-3k1-1,
解方程组
|
得x2+(2+k1)x-3k1-4=0,
由题意得-2-k1=4,
∴k1=-6,
∴△=-40<0,
∴方程无实数根,
∴方程组无实数解;
∴满足条件的直线不存在.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
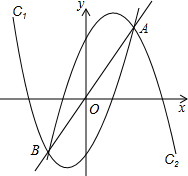 过C2顶点M的直线为l,且l与x轴交于点N.
过C2顶点M的直线为l,且l与x轴交于点N.
 +bx+c(a<0),如果抛物线同时经过点O、B、C:
+bx+c(a<0),如果抛物线同时经过点O、B、C: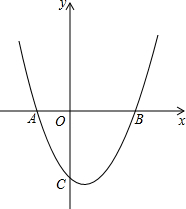
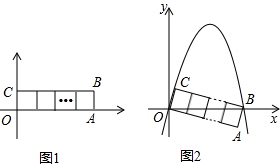
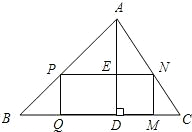 下再拼成(不计接缝用料及损耗)与长方形PQMN大小一样的长方形?若能,试给出一种拼法;若不能,试说明理由.
下再拼成(不计接缝用料及损耗)与长方形PQMN大小一样的长方形?若能,试给出一种拼法;若不能,试说明理由.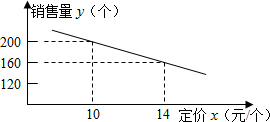 个星期的销售量y(个)与它的定价x(元/个)的关系如图所示:
个星期的销售量y(个)与它的定价x(元/个)的关系如图所示: