ĚâÄżÄÚČÝ
ČçÍĽŁ¬ÔÚÖ±˝Ç×ř±ęϵÖĐŁ¬µăCŁ¨
Ł¬0Ł©Ł¬µăDŁ¨0Ł¬1Ł©Ł¬CDµÄÖĐ´ąĎß˝»CDÓÚµăEŁ¬˝»yÖáÓÚµăBŁ¬µăP´ÓµăCłö·˘ŃŘCO·˝ĎňŇÔĂżĂë2
¸öµĄÎ»µÄËٶČÔ˶ŻŁ¬Í¬Ę±µăQ´ÓÔµăOłö·˘ŃŘOD·˝ĎňŇÔĂżĂë1¸öµĄÎ»µÄËٶČĎňµăDÔ˶ŻŁ¬µ±µăQµ˝´ďµăDʱŁ¬µăPŁ¬QͬʱֹͣÔ˶ŻŁ¬ÉčÔ˶ŻµÄʱĽäÎŞĂ룮
Ł¨1Ł©ÇółöµăBµÄ×ř±ęŁ»
Ł¨2Ł©µ±tÎŞşÎֵʱŁ¬ˇ÷POQÓëˇ÷CODĎŕËĆŁż
Ł¨3Ł©µ±µăPÔÚxÖḺ°ëÖáÉĎʱŁ¬ĽÇËıßĐÎPBEQµÄĂć»ýÎŞSŁ¬ÇóSąŘÓÚtµÄşŻĘýąŘϵʽŁ¬˛˘Đ´łö×Ô±äÁżµÄȡֵ·¶Î§Ł»
Ł¨4Ł©ÔÚµăPˇ˘QµÄÔ˶ŻąýłĚÖĐŁ¬˝«ˇ÷POQČƵăOĐýת180ˇăŁ¬µăPµÄ¶ÔÓ¦µăPˇäŁ¬µăQµÄ¶ÔÓ¦µăQˇäŁ¬µ±Ď߶ÎPˇäQˇäÓëĎ߶ÎBEÓĐą«ą˛µăʱŁ¬Ĺ×ÎďĎßy=ax2+1ľąýPˇäQˇäµÄÖе㣬´ËʱµÄĹ×ÎďĎßÓëxÖáŐý°ëÖá˝»ÓÚµăMŁ®ÓÉŇŃÖŞŁ¬Ö±˝ÓĐ´łöŁş˘ŮaµÄȡֵ·¶Î§ÎŞ______Ł»˘ÚµăMŇƶŻµÄĆ˝ľůËٶČĘÇ______Ł®

| 3 |
| 3 |
Ł¨1Ł©ÇółöµăBµÄ×ř±ęŁ»
Ł¨2Ł©µ±tÎŞşÎֵʱŁ¬ˇ÷POQÓëˇ÷CODĎŕËĆŁż
Ł¨3Ł©µ±µăPÔÚxÖḺ°ëÖáÉĎʱŁ¬ĽÇËıßĐÎPBEQµÄĂć»ýÎŞSŁ¬ÇóSąŘÓÚtµÄşŻĘýąŘϵʽŁ¬˛˘Đ´łö×Ô±äÁżµÄȡֵ·¶Î§Ł»
Ł¨4Ł©ÔÚµăPˇ˘QµÄÔ˶ŻąýłĚÖĐŁ¬˝«ˇ÷POQČƵăOĐýת180ˇăŁ¬µăPµÄ¶ÔÓ¦µăPˇäŁ¬µăQµÄ¶ÔÓ¦µăQˇäŁ¬µ±Ď߶ÎPˇäQˇäÓëĎ߶ÎBEÓĐą«ą˛µăʱŁ¬Ĺ×ÎďĎßy=ax2+1ľąýPˇäQˇäµÄÖе㣬´ËʱµÄĹ×ÎďĎßÓëxÖáŐý°ëÖá˝»ÓÚµăMŁ®ÓÉŇŃÖŞŁ¬Ö±˝ÓĐ´łöŁş˘ŮaµÄȡֵ·¶Î§ÎŞ______Ł»˘ÚµăMŇƶŻµÄĆ˝ľůËٶČĘÇ______Ł®

Ł¨1Ł©ÓÉĚâŇâµĂŁşOD=1Ł¬OC=
Ł¬ÓÉą´ąÉ¶¨ŔíµĂŁşDC=2Ł®
ˇßBEĘÇDCµÄÖĐ´ąĎߣ¬
ˇŕDE=1Ł¬ˇĎDEB=90ˇăŁ®
ÔÚˇ÷DEBÓëˇ÷DOCÖĐŁ¬
Ł¬
ˇŕˇ÷DEBˇŐˇ÷DOCŁ¨ASAŁ©Ł¬
ˇŕBD=DC=2Ł¬
ˇŕBO=1Ł¬
ˇŕBŁ¨0Ł¬-1Ł©Ł»
Ł¨2Ł©·ÖÁ˝ÖÖÇéżöŁş
˘Ůµ±µăPÔÚxÖáµÄŐý°ëÖáÉĎʱŁ¬
ÓÉŇŃÖŞµĂŁ¬CP=2
tŁ¬OP=CO-CP=
-2
tŁ¬OQ=tŁ®
ÓÉĚâŇâµĂŁş
=
»ň
=
Ł¬
Ľ´Łş
=
»ň
=
Ł¬
 ˝âµĂt=
˝âµĂt=
»ňt=
Ł»
˘Úµ±µăPÔÚxÖáµÄ¸ş°ëÖáÉĎʱŁ¬
ÓÉĚâŇâµĂŁş
=
»ň
=
Ł¬
Ľ´Łş
=
»ň
=
Ł¬
˝âµĂt=
»ňt=1Ł®
×ŰÉĎËůĘöŁşµ±t=
»ňt=
»ňt=
»ňt=1ʱŁ¬ˇ÷POQÓëˇ÷CODĎŕËĆŁ»
Ł¨3Ł©S=Sˇ÷PQB+Sˇ÷EQB=
(1+t)(2
t-
)+
(1+t)
=
t2+
t-
Ł¬
Ľ´SąŘÓÚtµÄşŻĘýąŘϵʽΪŁşS=
t2+
t-
Ł¬
ˇßµăPÔÚxÖḺ°ëÖáÉĎŁ¬
ˇŕtŁľ
Ł¬
Ó֡ߵ±µăQµ˝´ďµăDʱŁ¬µăPŁ¬QͬʱֹͣÔ˶ŻŁ¬¶řµăQÔ˶ŻĘ±ĽäÎŞ1Ă룬
ˇŕtˇÜ1Ł¬
ˇŕ×Ô±äÁżtµÄȡֵ·¶Î§ÎŞŁş
ŁĽtˇÜ1Ł»
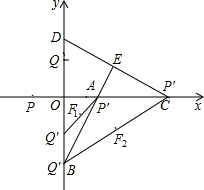 Ł¨4Ł©˘Ůµ±P'Q'ÓëBEÓĐą«ą˛µăʱŁ¬łőʼλÖõăPˇäÓëµăAÖغϣ¬AÎŞBEÓëxÖáµÄ˝»µăŁ®
Ł¨4Ł©˘Ůµ±P'Q'ÓëBEÓĐą«ą˛µăʱŁ¬łőʼλÖõăPˇäÓëµăAÖغϣ¬AÎŞBEÓëxÖáµÄ˝»µăŁ®
ÓÉŇŃÖŞµĂŁ¬OA=
Ł¬OPˇä=OP=2
t-
Ł¬
ˇŕ2
t-
=
Ł¬
ˇŕt=
Ł¬
ÖŐֹλÖõăPˇäÓëµăCÖغϣ¬µăQˇäÓëµăBÖغϣ¬Őâʱt=1Ł¬
ˇŕ
ˇÜtˇÜ1Ł®
ÉčP'Q'µÄÖеăÎŞFŁ¬µ±t=
ʱŁ¬F1(
Ł¬-
)Ł®
°Ń(
Ł¬-
)´úČëy=ax2+1Ł¬µĂŁşa=-16Ł®
µ±t=1ʱŁ¬F2(
Ł¬-
)Ł¬
°Ń(
Ł¬-
)´úČëy=ax2+1Ł¬µĂŁşa=-2Ł¬
ˇŕaµÄȡֵ·¶Î§ÎŞŁş-16ˇÜaˇÜ-2Ł»
˘ÚłőʼλÖõÄĹ×ÎďĎßÎŞy=-16x2+1Ł¬´ËʱM1(
Ł¬0)Ł¬
ÖŐֹλÖõÄĹ×ÎďĎßÎŞy=-2x2+1Ł¬´ËʱM2(
Ł¬0)Ł¬
ˇŕM1M2=
-
Ł¬
ˇßŇƶŻµÄʱĽäÎŞ
Ă룬
ˇŕµăMŇƶŻµÄĆ˝ľůËٶČÎŞĂżĂë(
-
)¸öµĄÎ»Ł®
ąĘ´đ°¸ÎŞ-16ˇÜaˇÜ-2Ł»ĂżĂë(
| 3 |
ˇßBEĘÇDCµÄÖĐ´ąĎߣ¬
ˇŕDE=1Ł¬ˇĎDEB=90ˇăŁ®
ÔÚˇ÷DEBÓëˇ÷DOCÖĐŁ¬
|
ˇŕˇ÷DEBˇŐˇ÷DOCŁ¨ASAŁ©Ł¬
ˇŕBD=DC=2Ł¬
ˇŕBO=1Ł¬
ˇŕBŁ¨0Ł¬-1Ł©Ł»
Ł¨2Ł©·ÖÁ˝ÖÖÇéżöŁş
˘Ůµ±µăPÔÚxÖáµÄŐý°ëÖáÉĎʱŁ¬
ÓÉŇŃÖŞµĂŁ¬CP=2
| 3 |
| 3 |
| 3 |
ÓÉĚâŇâµĂŁş
| OP |
| OD |
| OQ |
| OC |
| OP |
| OC |
| OQ |
| OD |
Ľ´Łş
| ||||
| 1 |
| t | ||
|
| ||||
|
| t |
| 1 |
 ˝âµĂt=
˝âµĂt=| 3 |
| 7 |
| 1 |
| 3 |
˘Úµ±µăPÔÚxÖáµÄ¸ş°ëÖáÉĎʱŁ¬
ÓÉĚâŇâµĂŁş
| OP |
| OD |
| OQ |
| OC |
| OP |
| OC |
| OQ |
| OD |
Ľ´Łş
2
| ||||
| 1 |
| t | ||
|
2
| ||||
|
| t |
| 1 |
˝âµĂt=
| 3 |
| 5 |
×ŰÉĎËůĘöŁşµ±t=
| 3 |
| 7 |
| 1 |
| 3 |
| 3 |
| 5 |
Ł¨3Ł©S=Sˇ÷PQB+Sˇ÷EQB=
| 1 |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
3
| ||
| 4 |
| ||
| 4 |
Ľ´SąŘÓÚtµÄşŻĘýąŘϵʽΪŁşS=
| 3 |
3
| ||
| 4 |
| ||
| 4 |
ˇßµăPÔÚxÖḺ°ëÖáÉĎŁ¬
ˇŕtŁľ
| 1 |
| 2 |
Ó֡ߵ±µăQµ˝´ďµăDʱŁ¬µăPŁ¬QͬʱֹͣÔ˶ŻŁ¬¶řµăQÔ˶ŻĘ±ĽäÎŞ1Ă룬
ˇŕtˇÜ1Ł¬
ˇŕ×Ô±äÁżtµÄȡֵ·¶Î§ÎŞŁş
| 1 |
| 2 |
 Ł¨4Ł©˘Ůµ±P'Q'ÓëBEÓĐą«ą˛µăʱŁ¬łőʼλÖõăPˇäÓëµăAÖغϣ¬AÎŞBEÓëxÖáµÄ˝»µăŁ®
Ł¨4Ł©˘Ůµ±P'Q'ÓëBEÓĐą«ą˛µăʱŁ¬łőʼλÖõăPˇäÓëµăAÖغϣ¬AÎŞBEÓëxÖáµÄ˝»µăŁ®ÓÉŇŃÖŞµĂŁ¬OA=
| ||
| 3 |
| 3 |
| 3 |
ˇŕ2
| 3 |
| 3 |
| ||
| 3 |
ˇŕt=
| 2 |
| 3 |
ÖŐֹλÖõăPˇäÓëµăCÖغϣ¬µăQˇäÓëµăBÖغϣ¬Őâʱt=1Ł¬
ˇŕ
| 2 |
| 3 |
ÉčP'Q'µÄÖеăÎŞFŁ¬µ±t=
| 2 |
| 3 |
| ||
| 6 |
| 1 |
| 3 |
°Ń(
| ||
| 6 |
| 1 |
| 3 |
µ±t=1ʱŁ¬F2(
| ||
| 2 |
| 1 |
| 2 |
°Ń(
| ||
| 2 |
| 1 |
| 2 |
ˇŕaµÄȡֵ·¶Î§ÎŞŁş-16ˇÜaˇÜ-2Ł»
˘ÚłőʼλÖõÄĹ×ÎďĎßÎŞy=-16x2+1Ł¬´ËʱM1(
| 1 |
| 4 |
ÖŐֹλÖõÄĹ×ÎďĎßÎŞy=-2x2+1Ł¬´ËʱM2(
| ||
| 2 |
ˇŕM1M2=
| ||
| 2 |
| 1 |
| 4 |
ˇßŇƶŻµÄʱĽäÎŞ
| 1 |
| 3 |
ˇŕµăMŇƶŻµÄĆ˝ľůËٶČÎŞĂżĂë(
3
| ||
| 2 |
| 3 |
| 4 |
ąĘ´đ°¸ÎŞ-16ˇÜaˇÜ-2Ł»ĂżĂë(



 +bx+cŁ¨aŁĽ0Ł©Ł¬ČçąűĹ×ÎďĎßͬʱľąýµăOˇ˘Bˇ˘CŁş
+bx+cŁ¨aŁĽ0Ł©Ł¬ČçąűĹ×ÎďĎßͬʱľąýµăOˇ˘Bˇ˘CŁş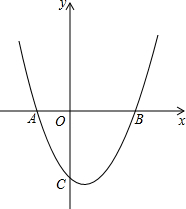



 y=x2-mx+nŁ¬Čô·˝łĚx2-mx+n=0Á˝¸ůµąĘýşÍÎŞ-2Ł®
y=x2-mx+nŁ¬Čô·˝łĚx2-mx+n=0Á˝¸ůµąĘýşÍÎŞ-2Ł®