Question

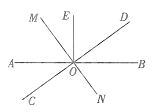
【题目】如图，∠AOB=30°，M，N分别是边OA，OB上的定点，P，Q分别是边OB，OA上的动点，记∠OPM=α，∠OQN=β，当MP+PQ+QN最小时，则关于α，β的数量关系正确的是（　　）

A. β﹣α=60° B. β+α=210° C. β﹣2α=30° D. β+2α=240°

Answer 1

【答案】B

【解析】

如图，作M关于OB的对称点M′，N关于OA的对称点N′，连接M′N′交OA于Q，交OB于P，则MP+PQ+QN最小易知∠OPM=∠OPM′=∠NPQ，∠OQP=∠AQN′=∠AQN，KD∠OQN=180°-30°-∠ONQ，∠OPM=∠NPQ=30°+∠OQP，∠OQP=∠AQN=30°+∠ONQ，由此即可解决问题．

如图，作M关于OB的对称点M′，N关于OA的对称点N′，连接M′N′交OA于Q，交OB于P，则MP+PQ+QN最小，

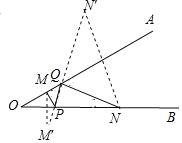
易知∠OPM=∠OPM′=∠NPQ，∠OQP=∠AQN′=∠AQN，

∵∠OQN=180°-30°-∠ONQ，∠OPM=∠NPQ=30°+∠OQP，∠OQP=∠AQN=30°+∠ONQ，

∴α+β=180°-30°-∠ONQ+30°+30°+∠ONQ=210°．

故选B．