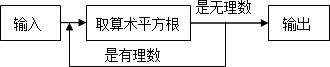
题目内容
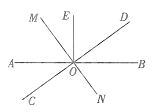
【题目】如图,直线AB,CD,OE⊥AB,过点O画直线MN⊥CD. 若点F是直线MN上任意一点(点O除外),且∠AOC=34°.求∠EOF的度数.
【答案】34°或146°
【解析】
当F在OM上时,根据垂直定义求出∠EOF=∠BOD,根据对顶角求出∠EOF=∠AOC,即可求出答案;当F在ON上时,求出∠AOM的度数,根据对顶角求出∠BON的度数,求出∠EOB+∠BON即可.
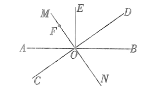
①当点F在射线OM上时,如图,
因为 OE⊥AB,MN⊥CD,
所以∠EOB=∠MOD=90°,
所以∠MOE+∠EOD=90°,∠EOD+∠BOD= 90°,
所以∠EOF=∠BOD=∠AOC=34°.
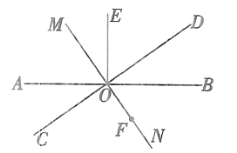
②当点F在射线ON上时,如图,
因为MN⊥CD,
所以 ∠MOC =∠AOC +∠AOM=90°,
所以 ∠AOM= 90°-34°=56°,
所以∠BON=∠AOM=56°
因为OE⊥AB,所以∠EOB=90°.
所以∠EOF=∠EOB+∠BON= 90°+56°=146°.
综上,∠EOF的度数是34°或146°.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目