题目内容
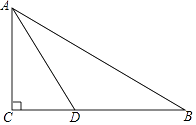
【题目】如图,某学生在旗杆EF与实验楼CD之间的A处,测得∠EAF=60°,然后向左移动10米到B处,测得∠EBF=30°,∠CBD=45°,tan∠CAD= ![]() .
. 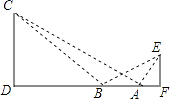
(1)求旗杆EF的高(结果保留根号);
(2)求旗杆EF与实验楼CD之间的水平距离DF的长.
【答案】
(1)解:∵∠EAF=60°,然后向左移动10米到B处,测得∠EBF=30°,∠CBD=45°,tan∠CAD= ![]() ,
,
∴tan60°= ![]() ,tan30°=
,tan30°= ![]() ,
,
解得,EF=5 ![]() ,AF=5,
,AF=5,
即旗杆EF的高为5 ![]() 米
米
(2)解:∵∠EAF=60°,然后向左移动10米到B处,测得∠EBF=30°,∠CBD=45°,tan∠CAD= ![]() ,AF=5,
,AF=5,
∴CD=BD, ![]() ,
,
设CD=3a,则BD=3a,AD=4a,
∴AB=a=10,
∴BD=3a=30,
∴DF=AD+AF=40+5=45,
即旗杆EF与实验楼CD之间的水平距离DF的长是45米
【解析】(1)根据题目中的数据和锐角三角函数可以求得EF和AF的长,从而可以解答本题;(2)根据题目中的数据和锐角三角函数可以求得AD和AF的长,从而可以得到旗杆EF与实验楼CD之间的水平距离DF的长.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目