Question

【题目】已知：如图所示，AC=CD，∠B=∠E=90°，AC⊥CD，则不正确的结论是（　　）

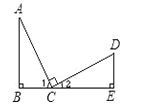
A. ∠1=∠2 B. ∠A =∠2 C. △ABC≌△CED D. ∠A与∠D互为余角

Answer 1

【答案】A

【解析】试题分析：A选项：因为AC⊥CD，∠ACD=90°，所以可得：∠1+∠2=90°，所以A选项错误；

B选项：因为AC⊥CD，∠ACD=90°，所以可得：∠1+∠2=90°，又因为∠B=90°，所以∠1+∠A=90°，根据同角的余角相等可得：∠A=∠2，故B选项正确；

C选项：因为AC⊥CD，∠ACD=90°，所以可得：∠1+∠2=90°，又因为∠B=90°，所以∠1+∠A=90°，根据同角的余角相等可得：∠A=∠2，又因为AC=CD,∠B=∠E，根据AAS可证△ABC≌△CED，故C选项正确；

D选项：因为AC⊥CD，∠ACD=90°，所以可得：∠1+∠2=90°，又因为∠B=90°，所以∠1+∠A=90°，根据同角的余角相等可得：∠A=∠2，因为∠E=90°，所以∠D+∠2=90°，所以∠A+∠D＝90°，所以∠A和∠D互为余角，故D选项正确.

故应选A.