题目内容
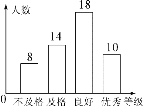
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF.
(1)求证:AD平分∠BAC;
(2)直接写出AB+AC与AE之间的等量关系.

【答案】(1)见解析;(2)见解析.
【解析】
(1)根据相“HL”定理得出△BDE≌△CDF,故可得出DE=DF,所以AD平分∠BAC;
(2)由(1)中△BDE≌△CDE可知BE=CF,AD平分∠BAC,故可得出△AED≌△AFD,所以AE=AF,故AB+AC=AE-BE+AF+CF=AE+AE=2AE.
(1)证明:∵DE⊥AB于E,DF⊥AC于F,
∴∠E=∠DFC=90°,
∴△BDE与△CDE均为直角三角形,
∵![]() ,
,
∴△BDE≌△CDF,
∴DE=DF,即AD平分∠BAC;
(2)AB+AC=2AE.
证明:∵BE=CF,AD平分∠BAC,
∴∠EAD=∠CAD,
∵∠E=∠AFD=90°,
∴∠ADE=∠ADF,
在△AED与△AFD中,
∵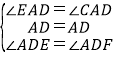 ,
,
∴△AED≌△AFD,
∴AE=AF,
∴AB+AC=AE-BE+AF+CF=AE+AE=2AE.

【题目】阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.如图是某校三个年级学生人数分布扇形统计图,其中八年级人数为408人,表是该校学生阅读课外书籍情况统计表.请你根据图表中的信息,解答下列问题:
图书种类 | 频数 | 频率 |
科普常识 | 840 | B |
名人传记 | 816 | 0.34 |
漫画丛书 | A | 0.25 |
其它 | 144 | 0.06 |
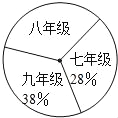
(1)求该校八年级的人数占全校总人数的百分率.
(2)求表中A,B的值.
(3)该校学生平均每人读多少本课外书?
【题目】某旅行社拟在暑假期间面向学生推出“林州红旗渠一日游”活动,
收费标准如下:
人数m | 0<m≤100 | 100<m≤200 | m>200 |
收费标准(元/人) | 90 | 85 | 75 |
甲、乙两所学校计划组织本校学生自愿参加此项活动.已知甲校报名参加的学生人数多于100人,乙校报名参加的学生人数少于100人.经核算,若两校分别组团共需花费10 800元,若两校联合组团只需花赞18 000元.
(1)两所学校报名参加旅游的学生人数之和超过200人吗? 为什么?
(2)两所学校报名参加旅游的学生各有多少人?