Question

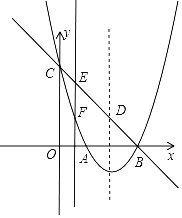
【题目】当x≤3时，函数y＝x2﹣2x﹣3的图象记为G，将图象G在x轴上方的部分沿x轴翻折，图象G的其余部分保持不变，得到一个新图象M，若直线y＝x+b与图象M有且只有两个公共点，则b的取值范围是_____．

Answer 1

【答案】﹣3＜b＜1或b＝﹣．

【解析】

根据题意画出图形，进而利用直线y＝x+b过（﹣1，0）以及（3，0）得出b的值，再利用直线y＝x+b与抛物线y＝x2﹣2x﹣3有一个交点，求出答案．

如图所示：∵y＝x2﹣2x﹣3，当y＝0，则0＝x2﹣2x﹣3，

解得：x1＝﹣1，x2＝3，

当直线y＝x+b过（﹣1，0）时，b＝1，

当直线y＝x+b过（3，0）时，b＝﹣3，

故当﹣3＜b＜1时，直线y＝x+b与图象M有且只有两个公共点，

当直线y＝x+b与抛物线y＝x2﹣2x﹣3有一个交点，

则x2﹣3x﹣3﹣b＝0有两个相等的实数根，

故△＝b2﹣4ac＝9+4（3+b）＝0，

解得：b＝﹣，

综上所述：直线y＝x+b与图象M有且只有两个公共点，则b的取值范是：﹣3＜b＜1或b＝﹣．

故答案为：﹣3＜b＜1或b＝﹣．