题目内容
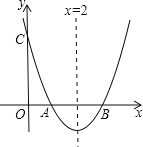
【题目】如图,已知抛物线![]() 与x轴交于点A,B,AB=2,与y轴交于点C,对称轴为直线x=2.
与x轴交于点A,B,AB=2,与y轴交于点C,对称轴为直线x=2.
(1)求抛物线的函数表达式;
(2)设P为对称轴上一动点,求△APC周长的最小值;
(3)设D为抛物线上一点,E为对称轴上一点,若以点A,B,D,E为顶点的四边形是菱形,则点D的坐标为 .
【答案】(1) ![]() ;(2)
;(2)![]() ;(3)(2,﹣1)
;(3)(2,﹣1)
【解析】
(1)根据抛物线对称轴的定义易求A(1,0),B(3,0),所以设抛物线的顶点式![]() ,将点A的坐标代入即可求得h,得到抛物线的函数表达式.
,将点A的坐标代入即可求得h,得到抛物线的函数表达式.
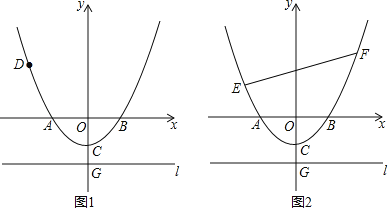
(2)如图1,连接AC、BC,BC交对称轴于点P,连接PA.根据抛物线的对称性质得到PA=PB,则△APC的周长的最小值=AC+AP+PC=AC+BC,所以根据两点间的距离公式来求该三角形的周长的最小值即可.
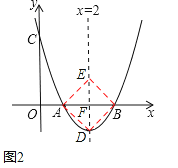
(3)如图2,根据“菱形ADBE的对角线互相垂直平分,抛物线的对称性”得到点D是抛物线![]() 的顶点坐标,即(2,﹣1).
的顶点坐标,即(2,﹣1).
解:(1)∵AB=2,对称轴为直线x=2,
∴点A的坐标是(1,0),点B的坐标是(3,0).
设抛物线的函数表达式为![]() ,
,
将A(1,0)代入得:![]() ,解得
,解得![]() .
.
∴抛物线的函数表达式为![]() ,即
,即![]() .
.
(2)如图1,连接AC、BC,BC交对称轴于点P,连接PA.
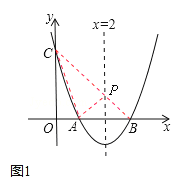
由(1)抛物线解析式为![]() ,A(1,0),B(3,0),
,A(1,0),B(3,0),
∴C(0,3).
∴![]() ,
,![]() .
.
∵点A、B关于对称轴x=2对称,∴PA=PB.∴PA+PC=PB+PC.此时,PB+PC=BC.
∴点P在对称轴上运动时,(PA+PB)的最小值等于BC.
∴△APC的周长的最小值=AC+AP+PC=AC+BC=![]() .
.
(3)如图2,根据“菱形ADBE的对角线互相垂直平分,抛物线的对称性”得到点D是抛物线y=x2-4x+3的顶点坐标,即(2,-1),
当E、D点在x轴的上方,即DE∥AB,AE=AB=BD=DE=2,此时不合题意,
故点D的坐标为:(2,-1).

 全能测控一本好卷系列答案
全能测控一本好卷系列答案