题目内容

【题目】(1)

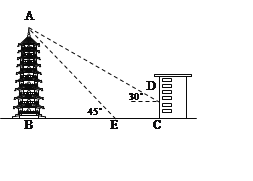
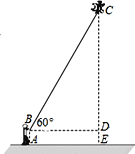
(2)如图，小方在清明假期中到郊外放风筝，风筝飞到C 处时的线长BC为20米，此时小方正好站在A处，并测得∠CBD=60°，牵引底端B离地面1.5米，求此时风筝离地面的高度.(,，结果精确到0.1米)

【答案】(1)1；(2)风筝离地面的高度约为18.8m．

【解析】

（1）代入特殊角的三角函数值直接计算即可；

（2）在Rt△BCD中，解直角三角形求出CD即可解决问题.

解：(1)cos245＋tan30·sin60

=

=

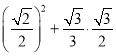
=1；

(2)在Rt△BCD中，BC=20米，∠CBD=60°，

则sin60°=，

∴CD=BC·sin60°=20·=10米，

又∵DE=AB=1.5米，

∴CE=CD+DE=10+1.5米

答：风筝离地面的高度约为米．

练习册系列答案
相关题目

【题目】在同一直角坐标系中，函数y＝mx＋m和函数y＝mx2＋2x＋2 (m是常数，且m≠0)的图象可能是（ ）

A.B.C.D.

【题目】如图，在平面直角坐标系中，抛物线交轴于，两点，与轴交于点.连接.

（1）求抛物线的解析式和点的坐标；

（2）“若点为第四象限内抛物线上一动点，点的横坐标为，的面积为，求关于的函数关系式，并求出的最大值；

（3）抛物线的对称轴上是否存在点，使为等腰三角形？若存在，请直接写出所有点的坐标；若不存在，请说明理由.

【题目】已知如图1，在以O为原点的平面直角坐标系中，抛物线y＝x2+bx+c与x轴交于A，B两点，与y轴交于点C（0，﹣1），连接AC，AO＝2CO，直线l过点G（0，t）且平行于x轴，t＜﹣1．

（1）求抛物线对应的二次函数的解析式；

（2）若D（﹣4，m）为抛物线y＝x2+bx+c上一定点，点D到直线l的距离记为d，当d＝DO时，求t的值．

（3）如图2，若E（﹣4，m）为上述抛物线上一点，在抛物线上是否存在点F，使得△BEF是直角三角形，若存在求出点F的坐标，若不存在说明理由．

【题目】如图，抛物线y＝ax2+bx+c（a≠0）的顶点坐标为（2，﹣1），图象与y轴交于点C（0，3），与x轴交于A、B两点．

（1）求抛物线的解析式；

（2）设抛物线对称轴与直线BC交于点D，连接AC、AD，点E为直线BC上的任意一点，过点E作x轴的垂线与抛物线交于点F，问是否存在点E使△DEF为直角三角形？若存在，求出点E坐标，若不存在，请说明理由．

【题目】下列说法中正确的是（ ）

A.“明天降雨的概率为”，表示明天有半天都在降雨

B.“抛一枚硬币，正面朝上的概率为”，表示每抛掷两次就有一次正面朝上

C.“抛一枚均匀的正方体骰子，朝上的点数是6的概率为”，表示随着抛掷次数的增加，“抛出朝上的点数是6”这一事件发生的概率稳定在 附近

D.某种彩票的中奖概率为，买1000张这种彩票一定有一张中奖

【题目】某风景区内有一古塔AB，在塔的北面有一建筑物，当光线与水平面的夹角是30°时，塔在建筑物的墙上留下了高3米的影子CD；而当光线与地面的夹角是45°时，塔尖A在地面上的影子E与墙角C有15米的距离（B、E、C在一条直线上），求塔AB的高度（结果保留根号）．

【题目】已知在Rt△ABC中，∠ACB=90°，现按如下步骤作图：

①分别以A，C为圆心，a为半径（a＞AC）作弧，两弧分别交于M，N两点；

②过M，N两点作直线MN交AB于点D，交AC于点E；

③将△ADE绕点E顺时针旋转180°，设点D的像为点F．

（1）请在图中直线标出点F并连接CF；

（2）求证：四边形BCFD是平行四边形；

（3）当∠B为多少度时，四边形BCFD是菱形．

【题目】某汽车在刹车后行驶的距离s(单位：米)与时间t(单位：秒)之间的关系得部分数据如下表：

时间t(秒)

0

0.2

0.4

0.6

0.8

1.0

1.2

…

行驶距离s(米)

0

2.8

5.2

7.2

8.8

10

10.8

…

假设这种变化规律一直延续到汽车停止．

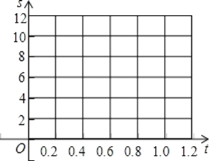
(1)根据这些数据在给出的坐标系中画出相应的点；

(2)选择适当的函数表示s与t之间的关系，求出相应的函数解析式；

(3)①刹车后汽车行驶了多长距离才停止?

②当t分别为t1,t2(t1<t2)时,对应s的值分别为s1,s2,请比较与的大小．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网