��Ŀ����
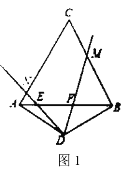
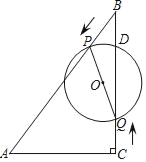
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬AC=6cm����ABC=30��������P�ӵ�B��������BA������ÿ��2cm���ٶ����A�����˶���ͬʱ����Q�ӵ�C��������CB������ÿ��![]() cm���ٶ����B�����˶����˶�ʱ��Ϊt�루0��t��6��������PQ����PQΪֱ������O��
cm���ٶ����B�����˶����˶�ʱ��Ϊt�루0��t��6��������PQ����PQΪֱ������O��
��1����t=1ʱ������BPQ�������
��2�����O�����Ϊy����y��t�ĺ�������ʽ��
��3������O��Rt��ABC��һ�������У���t��ֵ��
���𰸡���1����t=1ʱ��S��BPQ=![]() ����2��y=
����2��y=![]() t2��18��t+27�У���3������O��Rt��ABC��һ�������У�t��ֵΪ3��
t2��18��t+27�У���3������O��Rt��ABC��һ�������У�t��ֵΪ3��![]() ��0��
��0��![]()
��������
��1������DP��������BPM�ס�BAC���ɵ�PD=t��BQ=![]() ��6-t����Ȼ��õ�S��BPQ=
��6-t����Ȼ��õ�S��BPQ=![]() BQPD���ɵó����ۣ�
BQPD���ɵó����ۣ�
��2���ȱ�ʾ��DP��BD���������ù��ɶ������PQ��ƽ���������Բ�������ʽ���ɵó����ۣ�
��3���ֵ���O��BC���С���O��AB���У���O��AC����ʱ����������������ۼ��ɵó����ۣ�
��1����ͼ1��
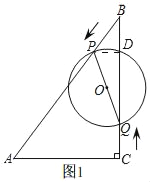
��Rt��ABC�У���ABC=30�㣬AC=6��
��AB=12��BC=6![]() ��
��
���˶�֪��BP=2t��CQ=![]() t��
t��
��BQ=BC��CQ=![]() ��6��t����
��6��t����
����DP��
��PQ�ǡ�O��ֱ����
���PDQ=90��
�ߡ�C=90�㣬
��PD��AC��
���BPD�ס�BAC��
��![]()
��![]() ��
��
��DP=t��BD=![]() t��
t��
S��BPQ=![]() BQPD=
BQPD=![]() ��
��![]() ��6��t��t=��
��6��t��t=��![]() t2+3
t2+3![]() t
t
�൱t=1ʱ��S��BPQ=��![]() +3
+3![]() =
=![]() ��
��
��2��DQ=|BQ��BD|=![]() ��6��t����
��6��t����![]() t|=2
t|=2![]() |3��t|��PQ2=PD2+DQ2=t2+[2
|3��t|��PQ2=PD2+DQ2=t2+[2![]() ��3��t��]2=13t2��72t+108��
��3��t��]2=13t2��72t+108��
��y=����![]() ��2=
��2=![]() t2��18��t+27��
t2��18��t+27��
��3�����˶�֪��BP=2t��CQ=![]() t��
t��
��BQ=BC��CQ=![]() ��6��t����
��6��t����
����O��BC����ʱ��PQ��BC��
���BPQ�ס�BAC��
��![]() ��
��
��![]() ��
��
��t1=3��
����O��AB����ʱ��PQ��AB��
���BPQ�ס�BCA
��![]() ��
��
��![]() ��
��
��t2=![]() ��
��
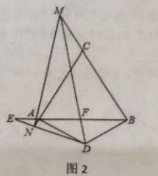
����O��AC����ʱ����ͼ2������O��OH��AC�ڵ�H����PD�ڵ�N��
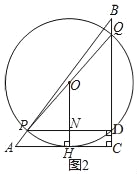
��OH��BC��
�ߵ�O��PQ���е㣬
��ON=![]() QD��
QD��
�ɣ�1��֪��BQ=![]() ��6��t����BD=
��6��t����BD=![]() t��
t��
��QD=BD��BQ=2![]() ��t��3����DC=BC��BD=6
��t��3����DC=BC��BD=6![]() ��
��![]() t=
t=![]() ��6��t��
��6��t��
��OH=ON+NH=![]() QD+DC=
QD+DC=![]() ��2
��2![]() ��t��3��+
��t��3��+![]() ��6��t��=3
��6��t��=3![]() ��
��
��PQ=2OH=6![]() ��
��
�ɣ�2��֪��PQ2=13t2��72t+108
��13t2��72t+108=36��3
���t3=0��t4=![]() ��
��
��������������O��Rt��ABC��һ�������У�t��ֵΪ3��![]() ��0��
��0��![]() ��
��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�