题目内容
【题目】四边形![]() 是由等边
是由等边![]() 和顶角为120°的等腰三角形
和顶角为120°的等腰三角形![]() 拼成,将一个60°角顶点放在点
拼成,将一个60°角顶点放在点![]() 处,60°角两边分别交直线
处,60°角两边分别交直线![]() 于
于![]() ,交直线
,交直线![]() 于
于![]() 两点.
两点.
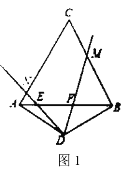
(1)当![]() 都在线段
都在线段![]() 上时,探究
上时,探究![]() 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;
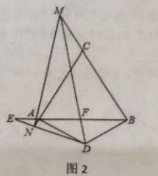
(2)当![]() 在边
在边![]() 的延长线上时,求证:
的延长线上时,求证:![]() .
.
【答案】(1)BM+AN=MN,证明见解析;(2)见解析;
【解析】
(1)把△DBM绕点D逆时针旋转120°得到△DAQ,根据旋转的性质可得DM=DQ,AQ=BM,∠ADQ=∠BDM,然后求出∠QDN=∠MDN,利用“边角边”证明△MND和△QND全等,根据全等三角形对应边相等可得MN=QN,再根据AQ+AN=QN整理即可得证;
(2)把△DAN绕点D顺时针旋转120°得到△DBP,根据旋转的性质可得DN=DP,AN=BP,根据∠DAN=∠DBP=90°可知点P在BM上,然后求出∠MDP=60°,然后利用“边角边”证明△MND和△MPD全等,根据全等三角形对应边相等可得MN=MP,从而得证;
(1)证明:∵四边形![]() 是由等边
是由等边![]() 和顶角为120°的等腰三角形
和顶角为120°的等腰三角形![]() 拼成,
拼成,
∴∠CAD=∠CBD=60°+30°=90°
把△DBM绕点D逆时针旋转120°得到△DAQ,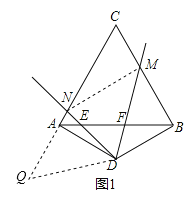
则DM=DQ,AQ=BM,∠ADQ=∠BDM,∠CBD=∠QAD =90°
∴∠CAD+∠QAD =180°
∴N、A、Q三点共线
∵∠QDN=∠ADQ+∠ADN=∠BDM+∠ADN=∠ABD-∠MDN=120°-60°=60°,
∴∠QDN=∠MDN=60°,
∵在△MND和△QND中,
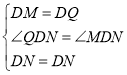
∴MN=QN,
∵QN=AQ+AN=BM+AN,
∴BM+AN=MN;
(2)MN+AN=BM.
理由如下:如图,把△DAN绕点D顺时针旋转120°得到△DBP,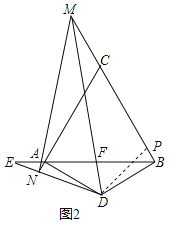
则DN=DP,AN=BP,
∵∠DAN=∠DBP=90°,
∴点P在BM上,
∵∠MDP=∠ADB-∠ADM-∠BDP=120°-∠ADM-∠ADN=120°-∠MDN=120°-60°=60°,
∴∠MDP=∠MDN=60°,
∵在△MND和△MPD中,

∴△MND≌△MPD(SAS),
∴MN=MP,
∵BM=MP+BP,
∴MN+AN=BM;
∴MN=BM -AN;

 初中学业考试导与练系列答案
初中学业考试导与练系列答案