Question

【题目】如图，锐角△ABC 中 BC＝a，AC＝b，AB＝c，记三角形 ABC 的面积为 S．

(1)求证：S＝absinC;

(2)求证：.

Answer 1

【答案】(1)见解析；（2）见解析

【解析】

（1）过A作AH⊥BC于H，可得AH=b×sinC，依据三角形ABC的面积=×BC×AH，即可得到S=absinC；

（2）过点C作CD⊥AB于D，在Rt△ADC和Rt△BDC中，∠ADC=∠BDC=90°，可得sinA=，sinB=，由此可得．同理可证，进而得到结论．

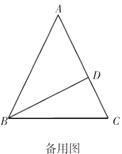
（1）如图，过A作AH⊥BC于H，则

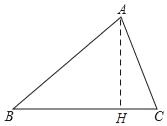
Rt△ACH中，sinC=，

∴AH=b×sinC，

∵三角形ABC的面积=×BC×AH，

∴S=absinC；

（2）如图，过点C作CD⊥AB于D，

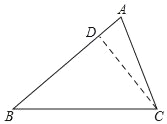
在Rt△ADC和Rt△BDC中，∠ADC=∠BDC=90°，

则sinA=，sinB=，

∴，,

∴．

过点A作AH⊥BC于H，同理可证．

∴ ．