Question

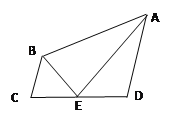
【题目】如图，在△ABC中，BA＝BC，CD和BE是△ABC的两条高，∠BCD＝45°，BE与CD交于点H．

（1）求证：△BDH≌△CDA；

（2）求证：BH＝2AE．

Answer 1

【答案】（1）见解析；（2）见解析．

【解析】

（1）依据BE是△ABC的高，可得∠BEA=∠BEC=90°，进而得到△BAE≌△BCE（ASA）；

（2）根据全等三角形的性质得到BH=AC，根据直角三角形的性质得到AC=2AE，BH=2AE，即可得到结论．

（1）∵∠BDC＝90°，∠BCD＝45°，

∴∠CBD＝45°，BD＝CD，

∵∠BDH＝∠CEH＝90°，∠BHD＝∠CHE，

∴∠DBH＝∠DCA，

在△BDH与△CDA中，

，

∴△BDH≌△CDA（ASA）；

（2）∵△BDH≌△CDA，

∴BH＝AC，

∵由题意知，△ABC是等腰三角形

∴AC＝2AE，

∴BH＝2AE．