题目内容
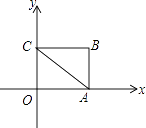
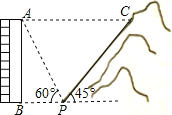
【题目】如图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡角为45°的山坡向上走到C处,这时,PC=30 m,点C与点A恰好在同一水平线上,点A、B、P、C在同一平面内。
(1)求居民楼AB的高度;
(2)求C、A之间的距离。(精确到0.1m,参考数据: ![]() )
)
【答案】(1)居民楼AB的高度为21.2m;
(2)C、A之间的距离为33.4m。
【解析】(1)首先分析图形:根据题意构造直角三角形,利用在Rt△CPE中,由sin45°=CEPC ,得出EC的长度,进而可求出答案.(2)在Rt△CPE中,tan60°=AB BP
,得出BP的长,进而得出PE的长,即可得出答案.
解:(1)过点C作CE⊥BP于点E,
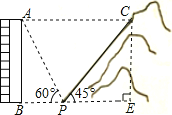
在Rt△CPE中
∵PC=30m,∠CPE=45°,
∴sin45°=![]() ,
,
∴CE=PCsin45°=30×![]() =15m,
=15m,
∵点C与点A在同一水平线上,
∴AB=CE=15![]() ≈21.2m,
≈21.2m,
答:居民楼AB的高度约为21.2m;
(2)在Rt△ABP中,∵∠APB=60°,
∴tan60°=![]() ,
,
∴BP=![]() m,
m,
∵PE=CE=15 m,
∴AC=BE=15![]() +5
+5![]() ≈33.4m,
≈33.4m,
答:C、A之间的距离约为33.4m.
“点睛”此题主要考查了仰角、坡角问题的应用,要求学生借助仰角、坡角关系构造直角三角形,并结合图形利用三角函数求解.

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案【题目】某校组织“大手拉小手,义卖献爱心”活动,购买了黑白两种颜色的文化衫共![]() 件,进行手绘设计后出售,所获得利润全部捐给山区困难孩子.每件文化衫的批发价和零售价如下表:
件,进行手绘设计后出售,所获得利润全部捐给山区困难孩子.每件文化衫的批发价和零售价如下表:
批发价(元) | 零售(元) | |
黑色文化衫 |
|
|
白色文化衫 |
|
|
(![]() )当
)当![]() ,
, ![]() ,假设文化衫全部售出,共获利
,假设文化衫全部售出,共获利![]() 元,求黑白两种文化衫各多少件?
元,求黑白两种文化衫各多少件?
(![]() )假设文化衫全部售出,其中卖出了黑色文化衫
)假设文化衫全部售出,其中卖出了黑色文化衫![]() 件,要获得
件,要获得![]() 元,请求出
元,请求出![]() 与
与![]() 的关系式.
的关系式.
【题目】已知关于x的方程(x-3)(x-2)-p2=0.
(1)求证:无论p取何值时,方程总有两个不相等的实数根;
(2)设方程两实数根分别为x1、x2,且满足x12+x22=3 x1x2,求实数p的值.
【题目】为响应市教育局倡导的“阳光体育运动”的号召,全校学生积极参与体育运动.为了进一步了解学校九年级学生的身体素质情况,体育老师在九年级800名学生中随机抽取50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,如下所示:
组别 | 次数x | 频数(人数) |
第1组 | 80≤x<100 | 6 |
第2组 | 100≤x<120 | 8 |
第3组 | 120≤x<140 | a |
第4组 | 140≤x<160 | 18 |
第5组 | 160≤x<180 | 6 |
请结合图表完成下列问题:
(1)表中的a=______;(2)请把频数分布直方图补充完整;
(3)这个样本数据的中位数落在第______组;
(4)若九年级学生一分钟跳绳次数(x)达标要求是:x<120为不合格;120≤x<140为合格;140≤x<160为良;x≥160为优.根据以上信息,请你估算学校九年级同学一分钟跳绳次数为优的人数为______.