题目内容
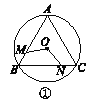
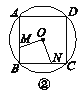
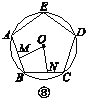
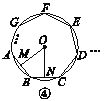
【题目】如图①②③④,M,N分别是⊙O的内接正三角形ABC,正方形ABCD,正五边形ABCDE,…,正n边形ABCDEFG…的边AB,BC上的点,且BM=CN,连接OM,ON.
(1)求图①中∠MON的度数;
(2)图②中,∠MON的度数是________,图③中∠MON的度数是________;
(3)试探究∠MON的度数与正n边形的边数n的关系(直接写出答案).
【答案】 90° 72°
【解析】(1)先分别连接OB、OC,可求出∠BOM=∠NOC,故∠MON=∠BOC,再由圆周角定理即可求出∠BOC=120°;
(2)同(1)即可解答;
(3)由(1)、(2)找出规律,即可解答.
(1)方法一:如图①,连接OB,OC.

图①
∵正三角形ABC内接于⊙O,
∴∠OBM=∠OCN=30°,∠BOC=120°.
又∵BM=CN,OB=OC,
∴△OBM≌△OCN,
∴∠BOM=∠CON,
∴∠MON=∠BOC=120°.
方法二:如图②,连接OA,OB.

图②
∵正三角形ABC内接于⊙O,
∴AB=BC,∠OAM=∠OBN=30°,∠AOB=120°.
∵BM=CN,∴AM=BN.
又∵OA=OB,∴△AOM≌△BON,
∴∠AOM=∠BON,
∴∠MON=∠AOB=120°.
(2)90° 72° (3)∠MON=![]() .
.

练习册系列答案
相关题目