题目内容
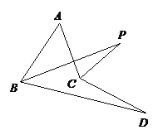
【题目】如图，∠ABD、∠ACD的角平分线交于点P，若∠A = 50°,∠D =10°，则∠P的度数为( )
A.15°B.20°C.25°D.30°
【答案】B
【解析】
利用三角形外角的性质，得到∠ACD与∠ABD的关系，然后用角平分线的性质得到角相等的关系，代入计算即可得到答案．
解：延长DC，与AB交于点E．
∵∠ACD是△ACE的外角，∠A=50°，
∴∠ACD=∠A+∠AEC=50°+∠AEC．
∵∠AEC是△BDE的外角，
∴∠AEC=∠ABD+∠D=∠ABD+10°，
∴∠ACD=50°+∠AEC=50°+∠ABD+10°，
整理得∠ACD-∠ABD=60°．
设AC与BP相交于O，则∠AOB=∠POC，
∴∠P+
∠ACD=∠A+∠ABD，
即∠P=50°-（∠ACD-∠ABD）=20°．
故选：B．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
