题目内容
【题目】如图,已知抛物线y=-![]() 与x轴交于A,B两点,与y轴交于点C,其中点A的坐标为(-3,0).
与x轴交于A,B两点,与y轴交于点C,其中点A的坐标为(-3,0).
(1)求b的值及点B的坐标;
(2)试判断△ABC的形状,并说明理由;
(3)一动点P从点A出发,以每秒2个单位的速度向点B运动,同时动点Q从点B出发,以每秒1个单位的速度向点C运动(当点P运动到点B时,点Q随之停止运动),设运动时间为t秒,当t为何值时,△PBQ与△ABC相似?
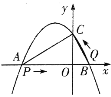
【答案】(1)![]() ,B的坐标为(1,0);(2)△ABC是直角三角形,理由见解析;(3)当t=1秒或
,B的坐标为(1,0);(2)△ABC是直角三角形,理由见解析;(3)当t=1秒或![]() 秒时,△PBQ与△ABC相似
秒时,△PBQ与△ABC相似
【解析】
(1)将点A的坐标代入![]() 中可解得b的值,由此可得抛物线的解析式,在所得解析式中令y=0得到关于x的方程,解方程即可求得点B的坐标;
中可解得b的值,由此可得抛物线的解析式,在所得解析式中令y=0得到关于x的方程,解方程即可求得点B的坐标;
(2)由(1)中所得抛物线的解析式可求得点C的坐标,结合点A、B的坐标可求得OA、OB、OC和AB的长度,这样由勾股定理可求得AC和BC的长,再证AB2=AC2+BC2可得△ABC是直角三角形;
(3)由题意用含t的代数式表达出BP和BQ的长度,结合∠ABC是公共角,∠ACB=90°,分∠PQB=90°和∠QPB=90°两种情况进行讨论即可求得△PBQ与△ABC相似时对应的t的值.
(1)将点A(-3,0)代入抛物线![]() 可得:
可得:![]() ,解得:
,解得:![]() ,
,
∴抛物线的解析式为:![]() ,
,
令y=0,得![]() ,解得x1=-3, x2=1,
,解得x1=-3, x2=1,
∴点B的坐标为:(1,0);
(2)△ABC是直角三角形,理由如下:
对于抛物线![]() ,令x=0,得y=
,令x=0,得y=![]() ,
,
∴点C的坐标为(0,![]() ),
),
∴OC=![]() ,OA=3,OB=1,AB=4,
,OA=3,OB=1,AB=4,
∴在Rt△AOC中,由勾股定理可得AC=![]() ,在Rt△COB中,由勾股定理可得BC=2,
,在Rt△COB中,由勾股定理可得BC=2,
∴AC2+BC2=12+4=16=AB2,
∴∠ACB=90°,
∴△ABC是直角三角形;
(3)由题意可得:AP=2t,BP=4-2t,BQ=t,CQ=2-t,
∵在△ABC和△PBQ中,∠ABC和∠PBQ是公共角,∠ACB=90°,
∴若△PBQ与△ABC相似,则∠PQB=90°或∠QPB=90°,
①当∠PQB=90°时,易得AC∥PQ,则△PQB~△ACB,
∴ ![]() ,即
,即![]() ,解得t=1;
,解得t=1;
②当∠QPB=90°,则△QPB~△ACB,
∴ ![]() ,即
,即![]() ,解得
,解得![]() ;
;
综上所述:当t=1秒或![]() 秒时,△PBQ与△ABC相似.
秒时,△PBQ与△ABC相似.

 名校课堂系列答案
名校课堂系列答案