题目内容
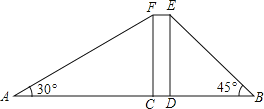
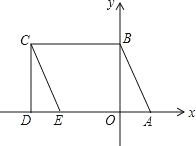
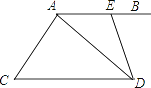
【题目】已知A(α,0)、B(b,0),点C在y轴上,且由|a+4|+(b-2)2=0.
(1)若S△ABC=6,求C点的坐标;
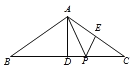
(2)将C向右平移,使OC平分∠ACB,点P是x轴上B点右边的一动点,PQ⊥OC于Q点.当∠ABC-∠BAC=60°时,求∠APQ的度数;
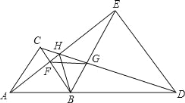
(3)在(2)的条件下,将线段AC平移,使其经过P点得线段EF,作∠APE的角平分线交OC的延长线于点M.当P点在x轴上运动时,求∠M-![]() ∠ABC的值.
∠ABC的值.


【答案】(1) C(0,2)或(0,-2);(2)∠APQ=30°;(3)∠M-![]() ∠ABC=0.
∠ABC=0.
【解析】
(1)根据已知条件求出点A,B的坐标,结合三角形的面积公式求出点C的纵坐标,即可求出点C的坐标.
(2)根据∠COB为![]() AOC的外角可得∠COB=∠BAC+
AOC的外角可得∠COB=∠BAC+![]() ∠ACB,后根据三角形内角和定理可用∠ABC和∠ACB表示∠COB,结合两式及∠ABC-∠BAC=60°即可求解.
∠ACB,后根据三角形内角和定理可用∠ABC和∠ACB表示∠COB,结合两式及∠ABC-∠BAC=60°即可求解.
(3)根据三角形内角和定理结合题(1)可得∠M+∠MPO=120°,后根据EF∥AC,∠BAC=∠APF以及PM平分∠OPE可得∠MPO=90°-![]() ∠BAC,再根据已知条件∠ABC-∠BAC=60°,结合三式即可求得∠M-
∠BAC,再根据已知条件∠ABC-∠BAC=60°,结合三式即可求得∠M-![]() ∠ABC的值.
∠ABC的值.
解:(1) 由已知条件 |a+4|+(b-2)2=0
可求得a=-4,b=2,即A(-4,0)、B(2,0)
S△ABC=![]() (|a|+b)c=6
(|a|+b)c=6
可求得c=2
即点C坐标为(0,2)或(0,-2).
(2) ∵∠COB=∠BAC+![]() ∠ACB;
∠ACB;
又∵∠COB=180°-∠ABC-![]() ∠ACB
∠ACB
∴2∠COB=180°+∠BAC-∠ABC,∠ABC-∠BAC=60°
∴∠COB=60°,∴∠APQ=30°
(3) 在△OMP中,∠M+∠MOP+∠MPO=180°,∠M+∠MPO=120°
∵EF∥AC,∴∠BAC=∠APF,
∴∠MPO=![]() (180°-∠APF )=90°-
(180°-∠APF )=90°-![]() ∠BAC,∠BAC=∠ABC-60°
∠BAC,∠BAC=∠ABC-60°
∴∠MPO=120°-![]() ∠ABC
∠ABC
∴∠M+120°-![]() ∠ABC=120°,∴∠M-
∠ABC=120°,∴∠M-![]() ∠ABC=0
∠ABC=0

 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案【题目】“十一”期间沈阳世博园(10月1日)的进园人数为![]() 万人,以后的6天里每天的进园人数变化如下表(正数表示比前一天多的人数负数表示比前一天少的人数,单位:万人)
万人,以后的6天里每天的进园人数变化如下表(正数表示比前一天多的人数负数表示比前一天少的人数,单位:万人)
日期 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
人数变化 |
|
|
|
|
|
|
(1)10月2日的进园人数是多少?
(2)10月1日-10月7日这7天内的进园人数最多的是哪天?最少的是哪天?它们相差多少?