题目内容
【题目】正方形
、
、
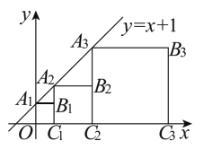
…按如图所示的方式放置.点
、
、
…和点
、
、
…别在直线
和
轴上，则点
的坐标是（ ）
A. 
B. 
C. 
D. 
【答案】B
【解析】
利用一次函数图象上点的坐标特征及正方形的性质可得出点
的坐标，根据点的坐标的变化可找出变化规律“点
的坐标为
（n为正整数）”，再代入n=2019即可得出的坐标，然后再将其横坐标减去纵坐标得到
的横坐标，和的纵坐标相同．
解：当
时，
，
∴点A1的坐标为（0，1）．
∵四边形A1B1C1O为正方形，
∴点B1的坐标为（1，1），点C1的坐标为（1，0）．
当
时，
，
∴点A2的坐标为（1，2）．
∵A2B2C2C1为正方形，
∴点B2的坐标为（3，2），点C2的坐标为（3，0）．
同理，可知：点B3的坐标为（7，4），点B4的坐标为（15，8），点B5的坐标为（31，16），…，
∴点的坐标为
（n为正整数），
∴点
的坐标为
，
∴点
的坐标为
，即为
．
故选：B．
练习册系列答案
相关题目
【题目】某学生本学期6次数学考试成绩如下表所示：
成绩类别 | 第一次月考 | 第二次月考 | 期中 | 第三次月考 | 第四次月考 | 期末 |
成绩/分 | 105 | 110 | 108 | 113 | 108 | 112 |
（1）6次考试成绩的中位数为 ，众数为 .
（2）求该生本学期四次月考的平均成绩.
（3）如果本学期的总评成绩按照月考平均成绩占20﹪、期中成绩占30﹪、期末成绩占50﹪计算，那么该生本学期的数学总评成绩是多少？
