题目内容

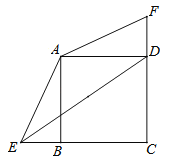
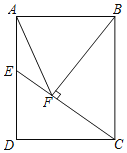
【题目】如图，点E是矩形ABCD的一边AD的中点，于F，连接AF；若，，则______．

【答案】

【解析】

延长CE交BA的延长线于点G，由题意可证△AGE≌△DCE，可得AG=CD=4，根据直角三角形的性质可得∠AFE=∠AGF，由勾股定理可求CG=10，即可求sin∠AFE的值．

延长CE交BA的延长线于点G．

∵四边形ABCD是矩形，∴AB∥CD，AB=CD=4，AD=BC=6，∴∠G=∠GCD，且AE=DE，∠AEG=∠DEC，∴△AGE≌△DCE（AAS），∴AG=CD=4，∴AG=AB，且BF⊥GF，∴AF=AG=AB=4，∴∠AFE=∠AGF．

∵BG=AG+AB=8，BC=6，∴GC10，∴sin∠AFE=sin∠AGF．

故答案为：．

练习册系列答案
相关题目

【题目】已知正方形ABCD中，BC=3，点E、F分别是CB、CD延长线上的点，DF=BE，连接AE、AF，过点A作AH⊥ED于H点．

（1）求证：△ADF≌△ABE；

（2）若BE=1，求tan∠AED的值．

【题目】如图，抛物线y=x2+ x+c与x轴的负半轴交于点A，与y轴交于点B，连结AB，点C（6，）在抛物线上，直线AC与y轴交于点D．

（1）求c的值及直线AC的函数表达式；

（2）点P在x轴正半轴上，点Q在y轴正半轴上，连结PQ与直线AC交于点M，连结MO并延长交AB于点N，若M为PQ的中点．

①求证：△APM∽△AON；

②设点M的横坐标为m，求AN的长（用含m的代数式表示）．

【题目】如图，已知二次函数的图像与轴的一个交点为 ，与轴的交点为，过的直线为.

（1）求二次函数的解析式及点的坐标；

（2）直接写出满足时，的取值 ；

（3）在两坐标轴上是否存在点，使得是以为底边的等腰三角形？若存在，求出的坐标；若不存在，说明理由.

【题目】如图，在Rt△ABC中，∠B=90°，AC=60，AB=30。点D是AC上的动点，过D作DF⊥BC于F，再过F作FE//AC，交AB于E。设CD=x，DF=y.

（1）求y与x的函数关系式；

（2）当四边形AEFD为菱形时，求x的值；

（3）当△FED是直角三角形时，求x的值.

【题目】如图，抛物线交x轴于A、B两点点A在点B的左边，交y轴于点C，直线经过点C与x轴交于点D，抛物线的顶点坐标为．

请你直接写出CD的长及抛物线的函数关系式；

求点B到直线CD的距离；

若点P是抛物线位于第一象限部分上的一个动点，则当点P运动至何处时，恰好使？请你求出此时的P点坐标．

【题目】如图，抛物线y＝x2﹣mx﹣（m+1）与x轴负半轴交于点A（x1，0），与x轴正半轴交于点B（x2，0）（OA＜OB），与y轴交于点C，且满足x12+x22﹣x1x2＝13．

（1）求抛物线的解析式；

（2）以点B为直角顶点，BC为直角边作Rt△BCD，CD交抛物线于第四象限的点E，若EC＝ED，求点E的坐标；

（3）在抛物线上是否存在点Q，使得S△ACQ＝2S△AOC？若存在，求出点Q的坐标；若不存在，说明理由．

【题目】美丽的甬江宛如一条玉带穿城而过，数学课外实践活动中，小林在甬江岸边的A， B两点处，利用测角仪分别对西岸的一观景亭D进行测量．如图，测得∠DAC=45°，∠DBC=65°，若AB=114米，求观景亭D到甬江岸边AC的距离约为多少米？

（参考数据：sin65°≈0.91，cos65°≈0.42，tan65°≈2.14）

【题目】已知二次函数的图象与x轴交于A、B两点，顶点为C．

当A、B两点的坐标分别为，时，求a、b满足的关系式．

若该函数图象的对称轴是直线，且为等腰直角三角形．

①求该二次函数的解析式用只含a的式子表示；

②在范围内任取三个自变量、、，所对应的三个函数值分别为、、，若以、、为长度的三条线段能围成三角形，求a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网