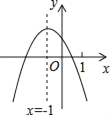
��Ŀ����
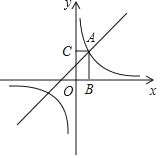
����Ŀ����ͼ��������y��x2��mx����m+1����x�Ḻ���ύ�ڵ�A��x1��0������x�������ύ�ڵ�B��x2��0����OA��OB������y�ύ�ڵ�C��������x12+x22��x1x2��13��
��1���������ߵĽ���ʽ��
��2���Ե�BΪֱ�Ƕ��㣬BCΪֱ�DZ���Rt��BCD��CD���������ڵ������ĵ�E����EC��ED�����E�����ꣻ
��3�������������Ƿ���ڵ�Q��ʹ��S��ACQ��2S��AOC�������ڣ������Q�����ꣻ�������ڣ�˵�����ɣ�

���𰸡���1��y��x2��2x��3����2��E������Ϊ��![]() ����
����![]() ������3����Q������Ϊ����3��12����2����3�������ɼ�����.
������3����Q������Ϊ����3��12����2����3�������ɼ�����.
��������
��1���ɸ���ϵ���Ĺ�ϵ�ɵ�x1+x2��m��x1x2������m+1��������x12+x22��x1x2��13�����m1��2��m2����5������OA��OB���ó������ߵĶԳ�����y���Ҳ࣬��ôm��2������ȷ�������ߵĽ���ʽ��
��2������BE��OE������ֱ��������б���ϵ����ߵ���б�ߵ�һ��ó�BE��![]() CD��CE������SSS֤����OBE�ա�OCE���ó���BOE����COE������E�ڵ������Ľ�ƽ�����ϣ���E������Ϊ��m����m��������y��x2��2x��3�����m��ֵ�����ɵõ�E�����ꣻ
CD��CE������SSS֤����OBE�ա�OCE���ó���BOE����COE������E�ڵ������Ľ�ƽ�����ϣ���E������Ϊ��m����m��������y��x2��2x��3�����m��ֵ�����ɵõ�E�����ꣻ
��3������Q��AC��ƽ���߽�x���ڵ�F������CF�����������ε������ʽ�ɵ�S��ACQ��S��ACF����S��ACQ��2S��AOC���ó�S��ACF��2S��AOC����ôAF��2OA��2��F��1��0�������ô���ϵ�������ֱ��AC�Ľ���ʽΪy����3x��3������AC��FQ������ֱ��FQ�Ľ���ʽΪy����3x+b����F��1��0�����룬���ô���ϵ�������ֱ��FQ�Ľ���ʽΪy����3x+3�������������ߵĽ���ʽ�������ó�������![]() ����⼴�ɵó���Q�����꣮
����⼴�ɵó���Q�����꣮
��1����������y��x2��mx����m+1����x�Ḻ���ύ�ڵ�A��x1��0������x�������ύ�ڵ�B��x2��0����
��x1+x2��m��x1x2������m+1����
��x12+x22��x1x2��13��
�ࣨx1+x2��2��3x1x2��13��
��m2+3��m+1����13��
��m2+3m��10��0��
���m1��2��m2����5��
��OA��OB��
�������ߵĶԳ�����y���Ҳ࣬
��m��2��
�������ߵĽ���ʽΪy��x2��2x��3��
��2������BE��OE��
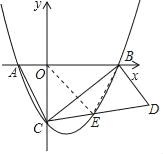
����Rt��BCD����CBD��90����EC��ED��
��BE��![]() CD��CE��
CD��CE��
��y��x2��2x��3��0�����x1����1��x2��3��
��A����1��0����B��3��0����
��C��0����3����
��OB��OC��
�֡�BE��CE��OE��OE��
���OBE�ա�OCE��SSS����
���BOE����COE��
���E�ڵ������Ľ�ƽ�����ϣ�
��E��������m����m������E��m����m������y��x2��2x��3��
��m��m2��2m��3�����m��![]() ��
��
�ߵ�E�ڵ������ޣ�
��E��������![]() ����
����![]() ����
����
��3������Q��AC��ƽ���߽�x���ڵ�F������CF����S��ACQ��S��ACF��
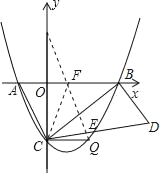
��S��ACQ��2S��AOC��
��S��ACF��2S��AOC��
��AF��2OA��2��
��F��1��0����
��A����1��0����C��0����3����
��ֱ��AC�Ľ���ʽΪy����3x��3��
��AC��FQ��
����ֱ��FQ�Ľ���ʽΪy����3x+b��
��F��1��0�����룬��0����3+b�����b��3��
��ֱ��FQ�Ľ���ʽΪy����3x+3��
����![]() ��
��
���![]() ��
��![]() ��
��
���Q����������3��12����2����3����