题目内容
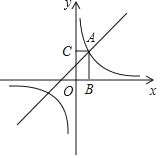
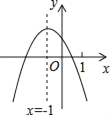
【题目】已知二次函数![]() 的图象与x轴交于A、B两点,顶点为C.
的图象与x轴交于A、B两点,顶点为C.
![]() 当A、B两点的坐标分别为
当A、B两点的坐标分别为![]() ,
,![]() 时,求a、b满足的关系式.
时,求a、b满足的关系式.
![]() 若该函数图象的对称轴是直线
若该函数图象的对称轴是直线![]() ,且
,且![]() 为等腰直角三角形.
为等腰直角三角形.
①求该二次函数的解析式![]() 用只含a的式子表示
用只含a的式子表示![]() ;
;
②在![]() 范围内任取三个自变量
范围内任取三个自变量![]() 、
、![]() 、
、![]() ,所对应的三个函数值分别为
,所对应的三个函数值分别为![]() 、
、![]() 、
、![]() ,若以
,若以![]() 、
、![]() 、
、![]() 为长度的三条线段能围成三角形,求a的取值范围.
为长度的三条线段能围成三角形,求a的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() .
.
【解析】
(1)将点A、B的坐标代入抛物线的解析式可得到关于a、b、c的方程组,然后消去字母c,从而可得到a、b之间的函数关系式;
(2)①先确定出抛物线的对称轴,然后可得到a、b之间的关系,接下来可求得顶点C的坐标(用含a、c的式子表示),然后再用点C的坐标表示出点B的坐标,最后将点B的坐标代入抛物线的解析式可得到关于a、c的方程,通过分解因式可得到a、c之间的关系,从而可得到抛物线的解析式;②先求得y的最大值和最小值,然后依据三角形的三边关系可列出关于a的不等式,从而可求得a的取值范围.
![]() 二次函数
二次函数![]() 的图象与x轴交于A、B两点,
的图象与x轴交于A、B两点,
![]() .
.
②-①得![]()
化简得:![]() .
.
![]() 该函数图象的对称轴是直线
该函数图象的对称轴是直线![]()
![]() ,
,
![]()
当![]() 时,
时,![]() .
.
![]() 且
且![]() .
.
![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,
![]()
![]() .
.
![]()
![]() .
.
![]() ,
,
![]() .
.
![]() .
.
![]() ,
,![]() ,
,
![]() 当
当![]() 或4时,y取得最小值
或4时,y取得最小值![]() ,
,
当![]() 时,y取得最大值
时,y取得最大值![]() .
.
若以![]() ,
,![]() ,
,![]() 为长度的三条线段能围成三角形
为长度的三条线段能围成三角形![]() 则
则![]() 且
且![]()
整理得:![]() 且
且![]() .
.
解得![]() .
.

练习册系列答案
相关题目