题目内容
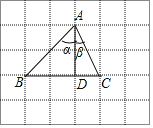
【题目】如图,在Rt△ABC中,∠B=90°,AC=60,AB=30。点D是AC上的动点,过D作DF⊥BC于F,再过F作FE//AC,交AB于E。设CD=x,DF=y.
(1)求y与x的函数关系式;
(2)当四边形AEFD为菱形时,求x的值;
(3)当△FED是直角三角形时,求x的值.

【答案】(1)![]() ;(2)40;(3)30.
;(2)40;(3)30.
【解析】
试题(1)由已知,根据锐角三角函数定义和特殊角的三角函数值可得∠C=30°,从而在Rt△CDF中,再应用锐角三角函数定义和特殊角的三角函数值可得y与x的函数关系式.
(2)根据菱形四边相等的性质,由AD=DF即AC-CD=DF列方程求解.
(3)首先判断△FED是直角三角形只有∠FDE=90°,得出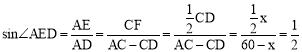 ,解之即为所求.
,解之即为所求.
试题解析:(1)∵∠B=90°,AC=60,AB=30,
∴![]() .∴∠C=30°.∴
.∴∠C=30°.∴![]() .
.
∴y与x的函数关系式为![]() .
.
(2)当四边形AEFD为菱形时,有AD=DF,
∴AC-CD=DF,即![]() ,解得x=40.
,解得x=40.
∴当四边形AEFD为菱形时,x=40.
(3)如图,当△FED直角三角形是时,只能是∠FDE=90°,
∵DF⊥BC,∠B=90°,∴DF//AB.
又∵FE//AC,∴四边形AEFD为平行四边形. ∴AE=DF.
由DF⊥BC得∠2=90°,∴∠1=∠2. ∴DE//BC.
∴∠3=∠B=90°,∠4=∠C=30°.
在Rt△BOC中,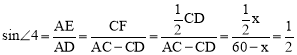 ,即60-x= x,
,即60-x= x,
∴x=30.
∴当△FED是直角三角形时,x=30.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目