题目内容
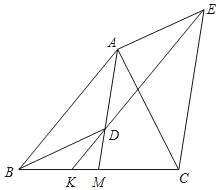
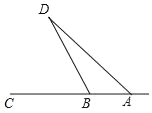
【题目】美丽的甬江宛如一条玉带穿城而过,数学课外实践活动中,小林在甬江岸边的A, B两点处,利用测角仪分别对西岸的一观景亭D进行测量.如图,测得∠DAC=45°,∠DBC=65°,若AB=114米,求观景亭D到甬江岸边AC的距离约为多少米?
(参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
【答案】214
【解析】
过点D作DE⊥AC,垂足为E,设BE=x,根据AE=DE,列出方程即可解决问题.
解:过点D作DE⊥AC,垂足为E,设BE=x,
在Rt△DEB中,tan∠DBE=![]() ,
,
∵∠DBC=65°,
∴DE=xtan65°.
又∵∠DAC=45°,
∴AE=DE.
∴114+x=xtan65°,
∴解得x≈100,
∴DE≈214(米).
∴观景亭D到甬江岸边AC的距离约为214米.

练习册系列答案
相关题目