题目内容
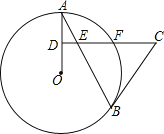
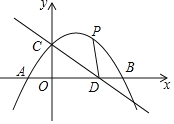
【题目】如图,抛物线交x轴于A、B两点![]() 点A在点B的左边
点A在点B的左边![]() ,交y轴于点C,直线
,交y轴于点C,直线![]() 经过点C与x轴交于点D,抛物线的顶点坐标为
经过点C与x轴交于点D,抛物线的顶点坐标为![]() .
.
![]() 请你直接写出CD的长及抛物线的函数关系式;
请你直接写出CD的长及抛物线的函数关系式;
![]() 求点B到直线CD的距离;
求点B到直线CD的距离;
![]() 若点P是抛物线位于第一象限部分上的一个动点,则当点P运动至何处时,恰好使
若点P是抛物线位于第一象限部分上的一个动点,则当点P运动至何处时,恰好使![]() ?请你求出此时的P点坐标.
?请你求出此时的P点坐标.
【答案】(1)CD=5,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)求出点C,D的坐标,再用勾股定理求得CD的长;设抛物线为y=a(x﹣2)2+4,将点C坐标代入求得a,即可得出抛物线的函数表达式;
(2)过点B直线CD的垂线,垂足为H.在Rt△BDH中,利用锐角三角函数即可求得点B到直线CD的距离;
(3)把点C(0,3)向上平移4个单位,向右平移3个单位得到点E(3,7),可得△OCD≌△FEC,则△DEC为等腰直角三角形,且∠EDC═45°,所以直线ED与抛物线的交点即为所求的点P,解方程组即可得出结论.
(1)∵![]() ,∴C(0,3),D(4,0).
,∴C(0,3),D(4,0).
∵∠COD=90°,∴CD![]() .
.
设抛物线为y=a(x﹣2)2+4,将点C(0,3)代入抛物线,得:3=4a+4,∴![]() ,∴抛物线的函数关系式为
,∴抛物线的函数关系式为![]() ;
;
(2)过点B作BH⊥CD于H,由![]() ,可得:x1=﹣2,x2=6,∴点B的坐标为(6,0).
,可得:x1=﹣2,x2=6,∴点B的坐标为(6,0).
∵OC=3,OD=4,CD=5,∴OB=6,从而BD=2.在Rt△DHB中,∵BH=BDsin∠BDH=BDsin∠CDO=2![]() ,∴点B到直线CD的距离为
,∴点B到直线CD的距离为![]() .
.
(3)把点C(0,3)向上平移4个单位,向右平移3个单位得到点E(3,7).
∵CF=OD=4,EF=OC=3,∠CFE=∠DOC=90°,∴△OCD≌△FEC,∴∠FCE=∠ODC,EC=DC,∴∠ECD=180°﹣(∠FCE+∠OCD)=180°﹣(∠ODC+∠OCD)=180°﹣90°=90°,∴△DEC为等腰直角三角形,且∠EDC═45°,因而,ED与抛物线的交点即为所求的点P.
由E(3,7),D(4,0),可得直线ED的解析式为:y=﹣7x+28,由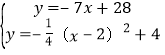 ,得
,得![]() (另一组解不合题意,已舍去.)
(另一组解不合题意,已舍去.)
所以,此时P点坐标为(![]() ).
).

【题目】某电器超市销售每台进价分别为2000元、1700元的A、B两种型号的空调,如表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 18000元 |
第二周 | 4台 | 10台 | 31000元 |
(进价、售价均保持不变,利润=销售总收入进货成本)
(1)求A、B两种型号的空调的销售单价;
(2)若超市准备用不多于54000元的金额再采购这两种型号的空调共30台,求A种型号的空调最多能采购多少台?