ΧβΡΩΡΎ»ί
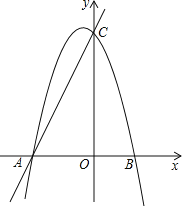
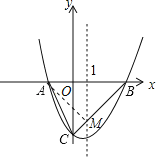
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ≈ΉΈοœΏLΘΚyΘΫax2+bx+cΘ®aΓΌ0Θ©”κx÷αΫΜ”ΎAΓΔBΝΫΒψΘ°”κy÷αΫΜ”ΎCΒψΘ°«“AΘ®©¹1Θ§0Θ©Θ§OBΘΫOCΘΫ3OAΘ°

Θ®1Θ©«σ≈ΉΈοœΏLΒΡΚ· ΐ±μ¥ο ΫΘΜ
Θ®2Θ©‘Ύ≈ΉΈοœΏLΒΡΕ‘≥Τ÷α…œ «Ζώ¥φ‘Ύ“ΜΒψMΘ§ ΙΓςACM÷ή≥ΛΉν–ΓΘΩ»τ¥φ‘ΎΘ§«σ≥ωΒψMΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
Θ®3Θ©Ν§Ϋ”ACΓΔBCΘ§‘Ύ≈ΉΈοœΏL…œ «Ζώ¥φ‘Ύ“ΜΒψNΘ§ ΙSΓςABCΘΫ2SΓςOCNΘΩ»τ¥φ‘ΎΘ§«σ≥ωΒψNΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©yΘΫx2©¹2x©¹3ΘΜΘ®2Θ©≈ΉΈοœΏΕ‘≥Τ÷α…œ¥φ‘ΎΒψMΘ®1Θ§©¹2Θ©ΖϊΚœΧβ“βΘΜΘ®3Θ©ΖϊΚœΧθΦΰΒΡΒψNΒΡΉχ±ξ «Θ®2Θ§©¹3Θ©ΜρΘ®©¹2Θ§5Θ©Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©‘Υ”Ο¥ΐΕ®œΒ ΐΖ®»ΖΕ®Κ· ΐΫβΈω ΫΦ¥Ω…ΘΜ
Θ®2Θ©ΒψB «ΒψAΙΊ”Ύ≈ΉΈοœΏΕ‘≥Τ÷αΒΡΕ‘≥ΤΒψΘ§‘Ύ≈ΉΈοœΏΒΡΕ‘≥Τ÷α…œ”–“ΜΒψMΘ§“Σ ΙMA+MCΒΡ÷ΒΉν–ΓΘ§‘ρΒψMΨΆ «BC”κ≈ΉΈοœΏΕ‘≥Τ÷αΒΡΫΜΒψΘ§άϊ”Ο¥ΐΕ®œΒ ΐΖ®«σ≥ω÷±œΏBCΒΡΫβΈω ΫΘ§Α―≈ΉΈοœΏΕ‘≥Τ÷αr=1¥ζ»κΦ¥Ω…«σΫβΘΜ
Θ®3Θ©…ηNΘ®xΘ§x2©¹2x©¹3Θ©Θ§ΗυΨί»ΐΫ«–ΈΒΡΟφΜΐΙΪ ΫΫβ¥πΦ¥Ω….
Θ®1Θ©”…AΘ®©¹1Θ§0Θ©Θ§OBΘΫOCΘΫ3OAΘ§ΒΟ
OBΘΫOCΘΫ3Θ§
Φ¥BΘ®3Θ§0Θ©Θ§CΘ®0Θ§©¹3Θ©Θ§
Α―AΘ§BΘ§CΒΡΉχ±ξ¥ζ»κΚ· ΐΫβΈω ΫΘ§ΒΟ
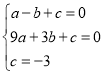 Θ§
Θ§
ΫβΒΟ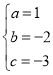 Θ§
Θ§
≈ΉΈοœΏΒΡΫβΈω ΫΈΣyΘΫx2©¹2x©¹3ΘΜ
Θ®2Θ©ΓΏΒψAΓΔBΙΊ”ΎΕ‘≥Τ÷αΕ‘≥ΤΘ§
ΓύΒψMΈΣBC”κΕ‘≥Τ÷αΒΡΫΜΒψ ±Θ§MA+MCΒΡ÷ΒΉν–ΓΘ°
…η÷±œΏBCΒΡΫβΈω ΫΈΣyΘΫkx+tΘ®kΓΌ0Θ©Θ§
‘ρ![]() Θ§
Θ§
ΫβΒΟΘΚ![]() Θ°
Θ°
Γύ÷±œΏACΒΡΫβΈω ΫΈΣyΘΫx©¹3Θ°
ΓΏ≈ΉΈοœΏΒΡΕ‘≥Τ÷αΈΣ÷±œΏxΘΫ1Θ°
ΓύΒ±xΘΫ1 ±Θ§yΘΫ©¹2Θ°
Γύ≈ΉΈοœΏΕ‘≥Τ÷α…œ¥φ‘ΎΒψMΘ®1Θ§©¹2Θ©ΖϊΚœΧβ“βΘΜ
Θ®3Θ©…ηNΘ®xΘ§x2©¹2x©¹3Θ©Θ§
ΓΏAΘ®©¹1Θ§0Θ©Θ§BΘ®3Θ§0Θ©Θ§
ΓύABΘΫ4Θ§OCΘΫ3Θ°
ΓύSΓςABCΘΫ![]() ABOCΘΫ
ABOCΘΫ![]() ΓΝ4ΓΝ3ΘΫ6Θ°
ΓΝ4ΓΝ3ΘΫ6Θ°
ΓΏSΓςABCΘΫ2SΓςOCNΘ§
Γύ2ΓΝ![]() OC|x|ΘΫ6Θ§Φ¥|x|ΘΫ2Θ§
OC|x|ΘΫ6Θ§Φ¥|x|ΘΫ2Θ§
ΫβΒΟxΘΫ2ΜρxΘΫ©¹2Θ°
Β±xΘΫ2 ±Θ§x2©¹2x©¹3ΘΫ©¹3Θ°¥Υ ±NΘ®2Θ§©¹3Θ©Θ°
Β±xΘΫ©¹2 ±Θ§x2©¹2x©¹3ΘΫ5Θ°¥Υ ±NΘ®©¹2Θ§5Θ©Θ°
Ήέ…œΥυ ωΘ§ΖϊΚœΧθΦΰΒΡΒψNΒΡΉχ±ξ «Θ®2Θ§©¹3Θ©ΜρΘ®©¹2Θ§5Θ©Θ°

 –¬ΜνΝΠΉήΕ·‘± νœΒΝ–¥πΑΗ
–¬ΜνΝΠΉήΕ·‘± νœΒΝ–¥πΑΗ Νζ»ΥΆΦ ιΩλά÷ΦΌΤΎ νΦΌΉς“Β÷Θ÷ί¥σ―ß≥ωΑφ…γœΒΝ–¥πΑΗ
Νζ»ΥΆΦ ιΩλά÷ΦΌΤΎ νΦΌΉς“Β÷Θ÷ί¥σ―ß≥ωΑφ…γœΒΝ–¥πΑΗ