题目内容
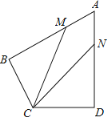
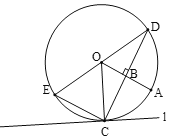
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径作
为直径作![]() ,点D在
,点D在![]() 上,
上,![]() ,
,![]() ,垂足为点E,
,垂足为点E,![]() 与
与![]() 和
和![]() 分别交于点M、F.连接
分别交于点M、F.连接![]() 、
、![]() 、
、![]() .
.

(1)证明:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求
,求![]() 的半径长;
的半径长;
(3)在(2)的条件下,求![]() 的长.
的长.
【答案】(1)证明见详解;(2)5;(3)2
【解析】
(1)易证BCOBDO,可得:∠BDO=∠BCO=90°,即:OD⊥BD,即可得证;
(2)由![]() ,得AE:ME:AM=1:2:
,得AE:ME:AM=1:2:![]() ,即AE=2,ME=4,连接CM,由tan∠ACM= tan∠AME=
,即AE=2,ME=4,连接CM,由tan∠ACM= tan∠AME=![]() ,可得:CM=
,可得:CM=![]() ,根据勾股定理得AC的长,即可得到结论;
,根据勾股定理得AC的长,即可得到结论;
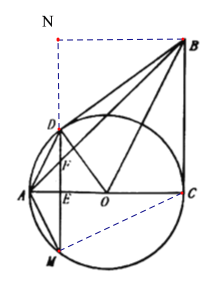
(3)过点B作BN∥AC,交MD的延长线于点N,设EF=x,由AEF~BNF,得NF=4x,从而得BC=NE=5x,BD=BC=5x,DN=NE-DE=5x-4,根据勾股定理,求出x的值,进而得到答案.
(1)在BCO和BDO中,
∵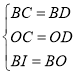
∴BCOBDO(SSS),
∴∠BDO=∠BCO=90°,即:OD⊥BD,
∴![]() 是
是![]() 的切线;
的切线;
(2)∵![]() ,
,
∴DE=ME,
∴AM=![]() ,
,
∵![]() ,
,
∴AE:ME:AM=1:2:![]() ,
,
∴AE=2,ME=4,
连接CM,则∠AMC=90°,
∵∠AME+∠CME=90°,
∠CME+∠ACM=90°,
∴∠AME=∠ACM,
∴tan∠ACM= tan∠AME=![]() ,
,
∴CM=2AM=2×![]() =
=![]() ,
,
∴AC=![]() ,
,
∴![]() 的半径长是:5.
的半径长是:5.
(3)过点B作BN∥AC,交MD的延长线于点N,
由(2)题可知:AE=2,EC=8,DE=ME=4,
∵四边形ECBN是矩形,
∴BN=EC=8,
设EF=x,
∵BN∥AC,
∴AEF~BNF,
∴![]() ,即:
,即:![]() ,
,
∴NF=4x,
∴BC=NE=5x,
∴BD=BC=5x,DN=NE-DE=5x-4,
∵在RtBND中,![]() ,
,
∴![]() ,解得:x=2,
,解得:x=2,
∴DF=DE-EF=4-2=2,

练习册系列答案
相关题目