Question

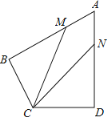
【题目】在四边形ABCD中，∠B＝∠C＝90°，若AB＝4，BC＝4，CD＝1，问：在BC上是否存在点P，使得AP⊥PD？若存在，求出BP的长；若不存在，请说明理由．

Answer 1

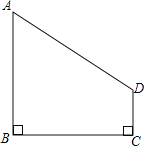
【答案】存在，理由见解析，BP＝2

【解析】

利用△ABP∽△PCD得出∠BPA+∠DPC＝90°，即∠APD＝90°，求出BP的长即可．

解：存在．

如图所示，

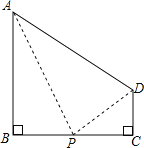
AP⊥PD，

∴∠APD＝90°，

∴∠APB+∠DPC＝90°，

又∵DC⊥BC，

∴∠DCP＝90°，

∴∠PDC+∠DPC＝90°，

∴∠APB＝∠PDC，

∵∠B＝∠C，

∴△ABP∽△PCD，

设BP＝x，则CP＝4﹣x，

即

即x（4﹣x）＝4，

则x2﹣4x+4＝0，

即（x﹣2）2＝0，

解得x＝2，即BP＝2．