题目内容
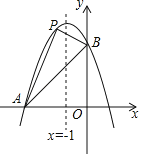
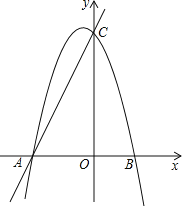
【题目】如图所示,已知直线y=kx+m与x轴、y轴分别交于A、C两点,抛物线y=﹣x2+bx+c经过A、C两点,点B是抛物线与x轴的另一个交点,当x=﹣![]() 时,y取最大值
时,y取最大值![]() .
.
(1)求抛物线和直线的解析式;
(2)设点P是直线AC上一点,且S△ABP:S△BPC=1:3,求点P的坐标;
(3)若直线y=![]() x+a与(1)中所求的抛物线交于M、N两点,问:
x+a与(1)中所求的抛物线交于M、N两点,问:
①是否存在a的值,使得∠MON=90°?若存在,求出a的值;若不存在,请说明理由;
②猜想当∠MON>90°时,a的取值范围(不写过程,直接写结论).
【答案】(1)y=﹣x2﹣x+6,y=2x+6;(2)点P(﹣![]() ,
,![]() )或P(﹣
)或P(﹣![]() ,﹣3);(3)①a=﹣3或a=
,﹣3);(3)①a=﹣3或a=![]() ,②﹣3<a<
,②﹣3<a<![]()
【解析】
(1)先根据直线的解析式求出A、C的坐标,然后将A、C的坐标代入抛物线中即可求出抛物线的解析式,进而可根据抛物线的解析式求出B点的坐标.
(2)根据等高三角形的面积比等于底边比,因此两三角形的面积比实际是AP:PC=1:3,即3AP=PC,可先求出AC的长,然后分情况讨论:
①当P在线段AC上时,AP+PC=AC,3AP=PC,据此可求出AP的长,然后根据∠CAB的三角函数值或通过构建相似三角形可求出P点的坐标.
②当P在CA的延长线上时,CP﹣AP=AC,3AP=PC,据此可求出AP的长,后面同①.
(3)①设直线y=![]() x+a与抛物线y=﹣x2﹣x+6的交点为M(xM,yM),N(xN,yN)(M在N左侧),由Rt△MM′O∽Rt△ON′N,推出
x+a与抛物线y=﹣x2﹣x+6的交点为M(xM,yM),N(xN,yN)(M在N左侧),由Rt△MM′O∽Rt△ON′N,推出 ![]() ,即MM′NN′=ON′OM′,推出﹣xMxN=yMyN,由方程组消去y整理,得:x2+
,即MM′NN′=ON′OM′,推出﹣xMxN=yMyN,由方程组消去y整理,得:x2+ ![]() x+a﹣6=0,再利用根与系数关系,列出方程即可解决问题.
x+a﹣6=0,再利用根与系数关系,列出方程即可解决问题.
②利用①的结果即可判断.
解:(1)当x=0时,y=6,
∴C(0,6),
当y=0时,x=﹣3,
∴A(﹣3,0),
∵抛物线y=﹣x2+bx+c经过点A、C,
∴![]() ,
,
解得:![]() .
.
∴抛物线的解析式为y=﹣x2﹣x+6,
当y=0时,整理得x2+x﹣6=0,
解得:x1=2,x2=﹣3,
∴点B(2,0).
(2)过点B作BD⊥AC,D为垂足,
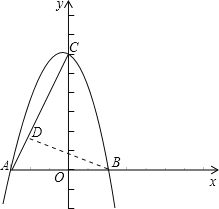
∵S△ABP:S△BPC=1:3,
∴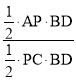 =
=![]() ,
,
∴AP:PC=1:3
由勾股定理,得AC=![]() =3
=3 ![]() ,
,
当点P为线段AC上一点时,过点P作PH⊥x轴,点H为垂足,
∵PH∥OC,
∴![]() =
=![]() ,
,
∴PH=![]() ,
,
∴![]() =2x+6,
=2x+6,
∴x=﹣![]() ,
,
∴点P(﹣![]() ,
,![]() )
)
当点P在CA延长线时,作PG⊥x轴,点G为垂足
∵AP:PC=1:3
∴AP:AC=1:2,
∴![]() =
=![]() ,
,
∴PG=3,
∴﹣3=2x+6
x=﹣![]() ,
,
∴点P(﹣![]() ,﹣3).
,﹣3).
(3)①存在a的值,使得∠MON=90°,
设直线y=![]() x+a与抛物线y=﹣x2﹣x+6的交点为M(xM,yM),N(xN,yN)(M在N左侧)
x+a与抛物线y=﹣x2﹣x+6的交点为M(xM,yM),N(xN,yN)(M在N左侧)
则  为方程组
为方程组 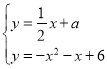 的解
的解
分别过点M、N作MM’⊥x轴,NN′⊥x轴,点M、N为垂足.
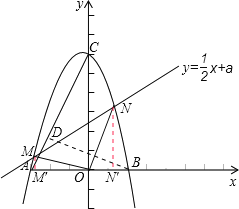
∴M′(xM,0),N′(xN,0),
∴OM′=﹣xMON′=xN
∵∠MON=90°,
∴∠MOM′+∠NON′=90°,
∵∠M′MO+∠MOM′=90°,
∴∠M’MO=∠NON’
∴Rt△MM′O∽Rt△ON′N,
∴![]() ,
,
∴MM′NN′=ON′OM′,
∴﹣xMxN=yMyN,
由方程组消去y整理,得:x2+![]() x+a﹣6=0.
x+a﹣6=0.
∴xM、xN是方程x2+![]() x+a﹣6=0的两个根,
x+a﹣6=0的两个根,
由根与系数关系得,xM+xN=﹣![]() ,xMxN=a﹣6
,xMxN=a﹣6
又∵yMyN=( ![]() xM+a)(
xM+a)( ![]() xN+a)=
xN+a)=![]() xMxN+
xMxN+![]() (xM+xN)+a2=
(xM+xN)+a2=![]() (a﹣6)﹣
(a﹣6)﹣![]() a+a2
a+a2
∴﹣(a﹣6)=![]() (a﹣6)﹣
(a﹣6)﹣![]() a+a2,
a+a2,
整理,得2a2+a﹣15=0
解得a1=﹣3,a2=![]() ,
,
∴存在a值,使得∠MON=90°,其值为a=﹣3或a=![]() .
.
②由①可知,当∠MON>90°时,a的取值范围为﹣3<a<![]() .
.

 快捷英语周周练系列答案
快捷英语周周练系列答案【题目】某地质量监管部门对辖区内的甲、乙两家企业生产的某同类产品进行检查,分别随机抽取了50件产品并对某一项关键质量指标做检测,获得了它们的质量指标值s,并对样本数据(质量指标值s)进行了整理、描述和分析.下面给出了部分信息.
a.该质量指标值对应的产品等级如下:
质量指标值 |
|
|
|
|
|
等级 | 次品 | 二等品 | 一等品 | 二等品 | 次品 |
说明:等级是一等品,二等品为质量合格(其中等级是一等品为质量优秀).
等级是次品为质量不合格.
b.甲企业样本数据的频数分布统计表如下(不完整).
c.乙企业样本数据的频数分布直方图如下.
甲企业样本数据的频数分布表
分组 | 频数 | 频率 |
| 2 | 0.04 |
| m | |
| 32 | n |
| 0.12 | |
| 0 | 0.00 |
合计 | 50 | 1.00 |
乙企业样本数据的频数分布直方图
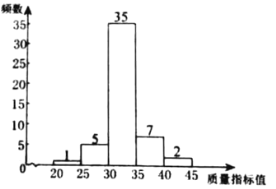
d.两企业样本数据的平均数、中位数、众数、极差、方差如下:
平均数 | 中位数 | 众数 | 极差 | 方差 | |
甲企业 | 31.92 | 32.5 | 34 | 15 | 11.87 |
乙企业 | 31.92 | 31.5 | 31 | 20 | 15.34 |
根据以上信息,回答下列问题:
(1)m的值为________,n的值为________.
(2)若从甲企业生产的产品中任取一件,估计该产品质量合格的概率为________;若乙企业生产的某批产品共5万件,估计质量优秀的有________万件;
(3)根据图表数据,你认为________企业生产的产品质量较好,理由为______________.(从某个角度说明推断的合理性)