题目内容
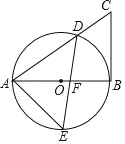
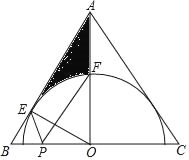
【题目】如图,在△ABC中,AB=AC,AO⊥BC于点O,OE⊥AB于点E,以点O为圆心,OE为半径作半圆,交AO于点F.
(1)求证:AC是⊙O的切线;
(2)若点F是OA的中点,OE=3,求图中阴影部分的面积;
(3)在(2)的条件下,点P是BC边上的动点,当PE+PF取最小值时,直接写出BP的长.
【答案】(1)详见解析;(2)![]() ;(3)当PE+PF取最小值时,BP的长为
;(3)当PE+PF取最小值时,BP的长为![]() .
.
【解析】
(1)作OH⊥AC于H,如图,利用等腰三角形的性质得AO平分∠BAC,再根据角平分线性质得OH=OE,然后根据切线的判定定理得到结论;
(2)先确定∠OAE=30°,∠AOE=60°,再计算出AE=3![]() ,然后根据扇形面积公式,利用图中阴影部分的面积=S△AOE-S扇形EOF进行计算;
,然后根据扇形面积公式,利用图中阴影部分的面积=S△AOE-S扇形EOF进行计算;
(3)作F点关于BC的对称点F′,连接EF′交BC于P,如图,利用两点之间线段最短得到此时EP+FP最小,通过证明∠F′=∠EAF′得到PE+PF最小值为3![]() ,然后计算出OP和OB得到此时PB的长.
,然后计算出OP和OB得到此时PB的长.
(1)证明:作OH⊥AC于H,如图,

∵AB=AC,AO⊥BC于点O,
∴AO平分∠BAC,
∵OE⊥AB,OH⊥AC,
∴OH=OE,
∴AC是⊙O的切线;
(2)∵点F是AO的中点,
∴AO=2OF=6,
而OE=3,
∴∠OAE=30°,∠AOE=60°,
∴AE=![]() OE=3
OE=3![]() ,
,
∴图中阴影部分的面积=S△AOE﹣S扇形EOF=![]() ×3×3
×3×3![]() ﹣
﹣![]() ;
;
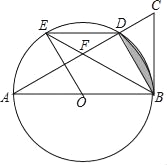
(3)作F点关于BC的对称点F′,连接EF′交BC于P,如图,
∵PF=PF′,
∴PE+PF=PE+PF′=EF′,此时EP+FP最小,
∵OF′=OF=OE,
∴∠F′=∠OEF′,
而∠AOE=∠F′+∠OEF′=60°,
∴∠F′=30°,
∴∠F′=∠EAF′,
∴EF′=EA=3![]() ,
,
即PE+PF最小值为3![]() ,
,
在Rt△OPF′中,OP=![]() OF′=
OF′=![]() ,
,
在Rt△ABO中,OB=![]() OA=
OA=![]() ×6=2
×6=2![]() ,
,
∴BP=2![]() ﹣
﹣![]() =
=![]() ,
,
即当PE+PF取最小值时,BP的长为![]() .
.