题目内容
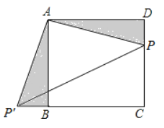
【题目】如图,四边形![]() 是正方形,点
是正方形,点![]() 在
在![]() 上,
上,![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 后能够与
后能够与![]() 重合,若
重合,若![]() ,
,![]() ,试求
,试求![]() 的长是__________.
的长是__________.
【答案】![]() .
.
【解析】
由正方形的性质得出AB=AD=3,∠ABC=∠D=∠BAD=90°,由勾股定理求出AP,再由旋转的性质得出△ADP≌△ABP′,得出AP′=AP=![]() ,∠BAP′=∠DAP,证出△PAP′是等腰直角三角形,得出PP′=
,∠BAP′=∠DAP,证出△PAP′是等腰直角三角形,得出PP′=![]() AP,即可得出结果.
AP,即可得出结果.
解:∵四边形ABCD是正方形,
∴AB=AD=3,DP=1,∠ABC=∠D=∠BAD=90°,
∴AP=![]() ,
,
∵△ADP旋转后能够与△ABP′重合,
∴△ADP≌△ABP′,
∴AP′=AP=![]() ,∠BAP′=∠DAP,
,∠BAP′=∠DAP,
∴∠PAP′=∠BAD=90°,
∴△PAP′是等腰直角三角形,
∴PP′=![]() AP=
AP=![]() ;
;
故答案为:![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目