题目内容
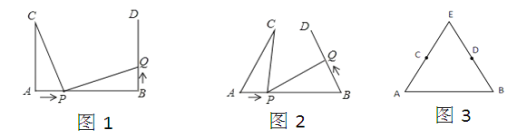
【题目】为丰富少年儿童的业余文化生活,某社区要在如图所示的AB所在的直线上建一图书阅览室,该社区有两所学校,所在的位置分别在点C和点D处。CA⊥AB于A,DB⊥AB于B,已知AB=25km,CA=15km,DB=10km,试问:阅览室E建在距A点多远时,才能使它到C、D两所学校的距离相等?
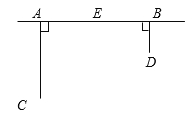
【答案】10 km
【解析】
把具体的位置关系转化成数学几何模型,找到等量关系,再设未知数,求出未知量即可.
解:设阅览室E到A的距离为x㎞.连结CE、DE.
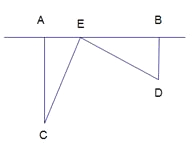
在Rt△EAC和Rt△EBD中,
CE2=AE2+AC2=x2+152,
DE2=EB2+DB2=(25-x)2+102.
因为点E到点CD的距离,所以CE=DE.
所以CE2=DE2.即x2+152=(25-x)2+102.
所以x=10.
因此,阅览室E应建在距A点10km处.

练习册系列答案
相关题目
【题目】某大酒店共有豪华间 50 间,实行旅游淡季、旺季两种价格标准:
淡季 | 旺季 | |
豪华间价格(元/天) | 600 | 800 |
(1)该酒店去年淡季,开始时,平均每天入住房间数为 20 间,后来,实行降价优惠提高豪华间入住率,每降低 20 元,每天入住房间数增加 1 间.如果豪华间的某日总收入为 12500 元,则该天的豪华间实际每间价格为多少元(同天的房间价格相同);
(2)该酒店豪华间的间数不变.经市场调查预测,如果今年旺季豪华间实行旺季价格,那么每天都客满;如果价格继续上涨,那么每增加 25 元,每天未入住房间数增加 1 间.不考虑其他因素,该酒店将豪华间的价格上涨多少元时, 豪华间的日总收入最高?最高日总收入是多少元?