��Ŀ����
����Ŀ���Ķ�̽�������������һ������A���Ƿ������һ������B�������ܳ�������ֱ�����֪�����ܳ��������һ�룿����������пո�
��1������֪����A�ı߳��ֱ�Ϊ6��1ʱ��С��ͬѧ�������о��ģ�
��������ε����߷ֱ���x��y��������÷����飺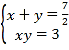 ����ȥy����ã�2x2��7x+6=0��
����ȥy����ã�2x2��7x+6=0��
�ߡ�=49��48��0��
��x1=_____��x2=_______��
������Ҫ��ľ���B���ڣ�
��2�������֪����A�ı߳��ֱ�Ϊ2��1���������С���ķ����о��Ƿ��������Ҫ��ľ���B��
��3���������A�ı߳�Ϊm��n�������о�����ʲô����ʱ������B���ڣ�
���𰸡���1��2��![]() ����2�������ڣ����ɼ���������3����m+n��2-8mn��0�����ɼ�����.
����2�������ڣ����ɼ���������3����m+n��2-8mn��0�����ɼ�����.
��������
���⣨1��ֱ�����������ʽ���㼴�ɣ�
��2�����գ�1���еĽⷨ���⼴�ɣ�
��3���ⷨͬ�ϣ����ø����б�ʽ�в��ȹ�ϵ����m��n�����������
�����������1�����Ͽ�֪��x-2����2x-3��=0��
��x1=2��x2=![]() .
.
��2�������ڣ��������£�
��������ε����߷ֱ���x��y�������⣬��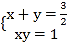 ��
��
��ȥy����2x2-3x+2=0.
�ߡ�=9-16��0���������ھ���B.
��3����m+n��2-8mn��0����������
��������ε����߷ֱ���x��y�������⣬��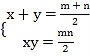 ��
��
��ȥy����2x2-��m+n��x+mn=0.
��=��m+n��2-8mn��0������m+n��2-8mn��0ʱ������Ҫ��ľ���B���ڣ�

 Ӧ������ҵ��ϵ�д�
Ӧ������ҵ��ϵ�д� �����ҵ��ٿ���������������ϵ�д�
�����ҵ��ٿ���������������ϵ�д�