题目内容
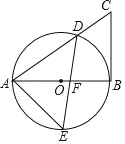
【题目】如图,AB是⊙O的直径,弦DE交AB于点F,⊙O的切线BC与AD的延长线交于点C,连接AE.
(1)试判断∠AED与∠C的数量关系,并说明理由;
(2)若AD=3,∠C=60°,点E是半圆AB的中点,则线段AE的长为 .
【答案】(1)∠AED=∠C(2)![]()
【解析】
(1)根据切线的性质和圆周角定理解答即可;
(2)根据勾股定理和三角函数进行解答即可.
(1)∠AED=∠C,证明如下:
连接BD,
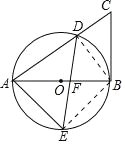
可得∠ADB=90°,
∴∠C+∠DBC=90°,
∵CB是⊙O的切线,
∴∠CBA=90°,
∴∠ABD+∠DBC=90°,
∴∠ABD=∠C,
∵∠AEB=∠ABD,
∴∠AED=∠C,
(2)连接BE,
∴∠AEB=90°,
∵∠C=60°,
∴∠CAB=30°,
在Rt△DAB中,AD=3,∠ADB=90°,
∴cos∠DAB=![]() ,
,
解得:AB=2![]() ,
,
∵E是半圆AB的中点,
∴AE=BE,
∵∠AEB=90°,
∴∠BAE=45°,
在Rt△AEB中,AB=2![]() ,∠ADB=90°,
,∠ADB=90°,
∴cos∠EAB=![]() ,
,
解得:AE=![]() .
.
故答案为:![]()

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目