题目内容
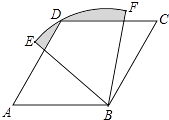
【题目】如图，将矩形ABCD绕点C顺时针旋转90°得到矩形FGCE，点M、N分别是BD、GE的中点，若BC=14，CE=2，则MN的长（ ）
A. 7 B. 8 C. 9 D. 10
【答案】D
【解析】分析：本题考查的是图形的旋转，矩形的性质和勾股定理.
解析：连接AC、CF、AF，∵矩形ABCD绕点C顺时针旋转90°得到矩形FFCE，∴∠ABC=90°，∴AC=
，AC=BD=GE=CF，AC与BD互相平分，GE与CF互相平分，∵点M、N分别是BD、GE的中点，∴M是AC的中点，N是CF的中点，∴MN是△ACF的中位线，∴MN=
AF，∵∠ACF=90°，∴△ACF是等腰直角三角形，∴AF=
AC=10
×
=20，∴MN=10．
故选D.
练习册系列答案
相关题目
