Question

【题目】某公司推出了一种高效环保型洗涤用品，年初上市后，公司经历了从亏损到盈利过程．下面的二次函数图象（部分）刻画了该公司年初以来累积利润s（万元）与销售时间t（月）之间的关系（即前t个月的利润总和s和t之间的关系）．根据图象提供的信息，解答下列问题：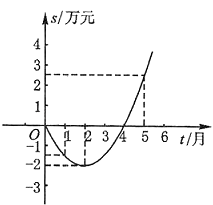
（1）由已知图象上的三点坐标，求累积利润s（万元）与时间t（月）之间的函数关系式；
（2）求截止到几月末公司累积利润可达到30万元；
（3）求第8个月公司所获利润是多少万元？

Answer 1

【答案】
（1）解：由图象可知其顶点坐标为（2，﹣2），

故可设其函数关系式为：S=a（t﹣2）2﹣2．

∵所求函数关系式的图象过（0，0），

于是得：

a（0﹣2）2﹣2=0，

解得a= ．

∴所求函数关系式为：S= （t﹣2）2﹣2，即S= t2﹣2t．

答：累积利润S与时间t之间的函数关系式为：S= t2﹣2t

（2）解：把S=30代入S= （t﹣2）2﹣2，

得 （t﹣2）2﹣2=30．

解得t1=10，t2=﹣6（舍去）．

答：截止到10月末公司累积利润可达30万元

（3）解：把t=7代入关系式，

得S= ×72﹣2×7=10.5，

把t=8代入关系式，

得S= ×82﹣2×8=16，

16﹣10.5=5.5，

答：第8个月公司所获利是5.5万元

【解析】（1）本题是通过构建函数模型解答销售利润的问题，应根据图象以及题目中所给的信息来列出S与t之间的函数关系式；（2）把S=30代入累计利润S= t2﹣2t的函数关系式里，求得月份；（3）分别t=7，t=8，代入函数解析S= t2﹣2t，再把总利润相减就可得出．