Question

【题目】已知在四边形ABCD中，∠ABC+∠ADC=180°，AB=BC．

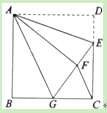
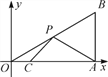
（1）如图1，若∠BAD=90°，AD=2，求CD的长度；

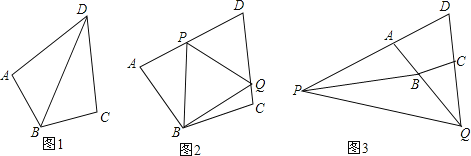
（2）如图2，点P、Q分别在线段AD、DC上，满足PQ=AP+CQ，求证：∠PBQ=90°∠ADC；

（3）如图3，若点Q运动到DC的延长线上，点P也运动到DA的延长线上时，仍然满足PQ=AP+CQ，则（2）中的结论是否成立？若成立，请给出证明过程，若不成立，请写出∠PBQ与∠ADC的数量关系，并给出证明过程.

Answer 1

【答案】（1）CD=2；（2）证明见解析；（3）（2）中结论不成立，应该是：，理由见解析.

【解析】

（1）如图1，利用HL证得两个直角三角形全等：Rt△BAD≌Rt△BCD，则其对应边相等：AD=DC=2；
（2）如图2，延长DC，在上面找一点K，使得CK=AP，连接BK，通过证△BPA≌△BCK（SAS）得到：∠1=∠2，BP=BK．然后由全等三角形△PBQ≌△BKQ的对应角相等求得∠PBQ=∠ABC，结合已知条件“∠ABC+∠ADC=180°”可以推知∠PBQ=90°-∠ADC；
（3）（2）中结论不成立，应该是：∠PBQ=90°+∠ADC．
如图3，在CD延长线上找一点K，使得KC=AP，连接BK，构建全等三角形：△BPA≌△BCK（SAS），由该全等三角形的性质和全等三角形的判定定理SSS证得：△PBQ≌△BKQ，则其对应角相等：∠PBQ=∠KBQ，结合四边形的内角和是360度可以推得：∠PBQ=90°+∠ADC．

（1）∵， ∴

在Rt△BAD和Rt△BCD中，

∴Rt△BAD≌Rt△BCD（HL）

∴AD=DC=2 ∴DC=2

（2）如图，延长DC，在上面找一点K，使得CK=AP，连接BK

∵

∴

∵

∴

在△BPA和△BCK中

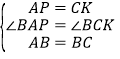
∴△BPA≌△BCK（SAS）

∴，BP=BK

∵PQ=AP+CQ

∴PQ=QK

在△PBQ和△BKQ中

∴△PBQ≌△BKQ（SSS）

∴

∴

∴

∵

∴

∴

∴

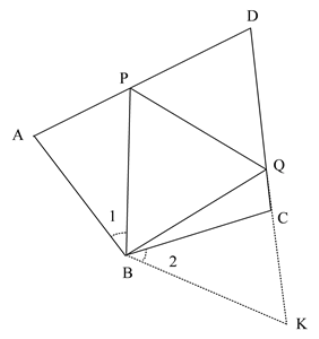
（3）（2）中结论不成立，应该是：

在CD延长线上找一点K，使得KC=AP，连接BK

∵

∴

∵

∴

在△BPA和△BCK中

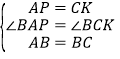
∴△BPA≌△BCK（SAS）

∴，BP=BK

∴

∵PQ=AP+CQ

∴PQ=QK

在△PBQ和△BKQ中

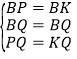
∴△PBQ≌△BKQ（SSS）

∴

∴

∴

∴