Question

【题目】四边形中，，，在、上分别找一点、，使三角形周长最小时，则的度数为（ ）

A. B. C. D.

Answer 1

【答案】C

【解析】

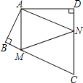
延长AB到A′使得BA′＝AB，延长AD到A″使得DA″＝AD，连接A′A″与BC、CD分别交于点M、N，此时△AMN周长最小，推出∠AMN＋∠ANM＝2（∠A′＋∠A″）即可解决．

延长AB到A′使得BA′＝AB，延长AD到A″使得DA″＝AD，连接A′A″与BC、CD分别交于点M、N，

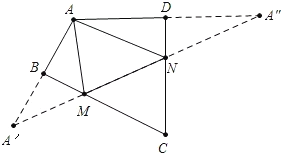
∵∠ABC＝∠ADC＝90°，

∴A、A′关于BC对称，A、A″关于CD对称，

此时△AMN的周长最小，

∵BA＝BA′，MB⊥AB，

∴MA＝MA′，同理：NA＝NA″，

∴∠A′＝∠MAB，∠A″＝∠NAD，

∵∠AMN＝∠A′＋∠MAB＝2∠A′，∠ANM＝∠A″＋∠NAD＝2∠A″，

∴∠AMN＋∠ANM＝2（∠A′＋∠A″），

∵∠BAD＝130°，

∴∠A′＋∠A″＝180°∠BAD＝50°

∴∠AMN＋∠ANM＝2×50°＝100°．

故选：C．